Question

已知函数f（x）=e^|x|+|x|．若关于x的方程f（x）=k有两个不同的实根，则实数k的取值范围是

1. A.
   （0，1）
2. B.
   （1，+∞）
3. C.
   （-1，0）
4. D.
   （-∞，-1）

Answer 1

B
分析：将方程f（x）=k恰有两个不同的实根，转化为方程e^|x|=k-|x|恰有两个不同的实根，再转化为一个函数y=e^|x|的图象与一条折线y=k-|x|的位置关系研究．
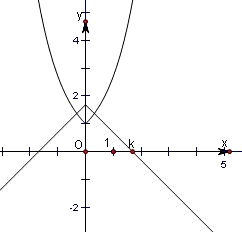
解答：解：方程f（x）=k化为：方程e^|x|=k-|x|
令 y=e^|x|，y=k-|x|，
y=k-|x|表示过斜率为1或-1的平行折线系，
折线与曲线y=e^|x|恰好有一个公共点时，有k=1，如图，
若关于x的方程f（x）=k有两个不同的实根，则实数k的取值范围是（1，+∞）．
故选B．
点评：本题主要考查根的存在性及根的个数判断，解答关键是利用直线与曲线的位置关系．