
分析 (1)由函数f(x)=x-1在区间[-2,1]上是增函数求出在[-2,1]上的值域,不满足在区间上封闭的概念;
(2)把给出的函数g(x)=$\frac{3x+a}{x+1}$变形为3+$\frac{a-3}{x+1}$,分a=3,a>3,a<3三种情况进行讨论,利用函数在区间[3,10]上封闭列式求出a的取值范围;
(3)假设h(x)=|1-$\frac{1}{x}$|在区间[a,b]上封闭,作出函数h(x)的图象,讨论a,b的取值范围,结合函数的单调性进行判断即可.
解答 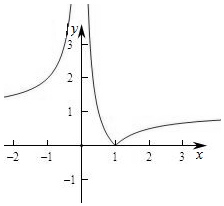 解:(1)f(x)=x-1在区间[-2,1]上单调递增,所以f(x)的值域为[-3,0]
解:(1)f(x)=x-1在区间[-2,1]上单调递增,所以f(x)的值域为[-3,0]
而[-3,0]?[-2,1],所以f(x)在区间[-2,1]上不是封闭的;
(2)因为g(x)=$\frac{3x+a}{x+1}$=3+$\frac{a-3}{x+1}$,
①当a=3时,函数g(x)的值域为{3}⊆[3,10],适合题意.
②当a>3时,函数g(x)=3+$\frac{a-3}{x+1}$在区间[3,10]上单调递减,故它的值域为$[\frac{30+a}{11},\frac{9+a}{4}]$,
由$[\frac{30+a}{11},\frac{9+a}{4}]$⊆[3,10],得$\left\{\begin{array}{l}{\frac{30+a}{11}≥3}\\{\frac{9+a}{4}≤10}\end{array}\right.$,解得3≤a≤31,故3<a≤31.
③当a<3时,在区间[3,10]上有$g(x)=\frac{3x+a}{x+1}=3+\frac{a-3}{x+1}<3$,显然不合题意.
综上所述,实数a的取值范围是3≤a≤31;
(3)作出函数h(x)=|1-$\frac{1}{x}$|的图象如图,则h(x)≥0,
当b<0时,定义域为[a,b],则不满足条件,
函数h(x)的定义域为{x|x≠0},
则必有a>0,
当a>1时,函数h(x)在[a,b]上为增函数,
此时h(b)=|1-$\frac{1}{b}$|=1-$\frac{1}{b}$<1,此时函数的值域[f(a),f(b)]?[a,b],此时不满足条件.
若0<a<1,b>1,此时函数在[a,b]上的最小值为h(1)=0,而a>0,此时不满足条件.
若0<a<b<1,此时函数h(x)在[a,b]上为减函数,
则函数的值域为[f(b),f(a)],即函数的值域为[$\frac{1}{b}$-1,$\frac{1}{a}$-1],
若[$\frac{1}{b}$-1,$\frac{1}{a}$-1]⊆[a,b],则满足$\left\{\begin{array}{l}{\frac{1}{b}-1≥a}\\{\frac{1}{a}-1≤b}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{1}{b}≥a+1}\\{\frac{1}{a}≤b+1}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{1}{b}≤-a-1}\\{\frac{1}{a}≤b+1}\end{array}\right.$,则$\frac{1}{a}$-$\frac{1}{b}$≤b-a,
即$\frac{b-a}{ab}$≤b-a,则$\frac{1}{ab}$≤1,则ab≥1,与0<a<b<1,ab<1矛盾,
综上不存在a,b,使函数h(x)=|1-$\frac{1}{x}$|在区间[a,b]上封闭.
点评 本题是新定义题,考查函数与方程的应用,考查了分类讨论得数学思想方法,解答此题的关键是正确分类,因该题需要较细致的分类,综合性较强,难度较大.


科目:高中数学 来源: 题型:填空题
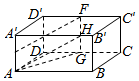 已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.
已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.
如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n⊥α,则m∥n | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com