Question

2．如图，四棱锥O-ABCD中，AC垂直平分BD，|$\overrightarrow{OB}$|=2，|$\overrightarrow{OD}$|=1，则（$\overrightarrow{OA}$+$\overrightarrow{OC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）的值是3．

Answer 1

分析 设AC、BD交于点E，由题意$\overrightarrow{OB}$+$\overrightarrow{OD}$=2$\overrightarrow{OE}$，$\overrightarrow{EA}$•$\overrightarrow{DB}$=$\overrightarrow{EC}$•$\overrightarrow{DB}$，由此即可求出（$\overrightarrow{OA}$+$\overrightarrow{OC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）的值．

解答 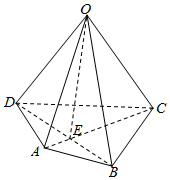解：如图所示，
四棱锥O-ABCD中，设AC、BD交于点E，
由题意AC⊥BD，DE=BE，
∴$\overrightarrow{OB}$+$\overrightarrow{OD}$=2$\overrightarrow{OE}$，$\overrightarrow{EA}$•$\overrightarrow{DB}$=$\overrightarrow{EC}$•$\overrightarrow{DB}$=0；
又|$\overrightarrow{OB}$|=2，|$\overrightarrow{OD}$|=1，
∴（$\overrightarrow{OA}$+$\overrightarrow{OC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）=（$\overrightarrow{OE}$+$\overrightarrow{EA}$+$\overrightarrow{OE}$+$\overrightarrow{EC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）
=（2$\overrightarrow{OE}$+$\overrightarrow{EA}$+$\overrightarrow{EC}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）
=2$\overrightarrow{OE}$•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）+（$\overrightarrow{EA}$+$\overrightarrow{EC}$）•$\overrightarrow{DB}$
=（$\overrightarrow{OB}$+$\overrightarrow{OD}$）•（$\overrightarrow{OB}$-$\overrightarrow{OD}$）
=${\overrightarrow{OB}}^{2}$-${\overrightarrow{OD}}^{2}$
=2²-1²
=3．
故答案为：3．

点评 本题考查了平面向量的线性运算与数量积的运算问题，是基础题目．