
| A. | (0,1) | B. | (-1,0) | C. | (-∞,0) | D. | (-∞,0)∪(1,+∞) |
分析 根据条件容易判断a≠0,从而可得出$f(x)=lg\frac{a(x-\frac{a+2}{a})}{x-1}$,根据f(x)为奇函数,定义域关于原点对称,从而讨论a的符号解不等式$\frac{a(x-\frac{a+2}{a})}{x-1}>0$,并满足该不等式的解集关于原点对称,这样便可求出a=-1,从而得出$f(x)=lg\frac{-(x+1)}{x-1}$,这样解不等式$lg\frac{-(x+1)}{x-1}<0$便可得出x的取值范围.
解答 解:a=0时,显然f(x)不是奇函数;
∴a≠0;
∴$f(x)=lg\frac{a(x-\frac{a+2}{a})}{x-1}$;
∵f(x)的定义域关于原点对称;
∴(1)若a>0,则$\frac{a+2}{a}>0$,∴不等式$\frac{a(x-\frac{a+2}{a})}{x-1}>0$的解集不关于原点对称;
即这种情况不存在;
(2)若a<0,则解$\frac{a(x-\frac{a+2}{a})}{x-1}>0$得,$\frac{a+2}{a}<x<1$;
∴$\frac{a+2}{a}=-1$;
解得a=-1,满足条件;
∴$f(x)=lg\frac{-(x+1)}{x-1}$;
∴解$lg\frac{-(x+1)}{x-1}<0$得:
$0<\frac{-(x+1)}{x-1}<1$;
解得-1<x<0;
∴使f(x)<0的x的取值范围是(-1,0).
故选:B.
点评 考查奇函数的定语,奇函数定义域关于原点对称的特点,以及分式不等式的解法,对数函数的单调性.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x>-\frac{2}{3}$ | B. | $x>-\frac{3}{2}$ | C. | $x<-\frac{2}{3}$ | D. | $x<-\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
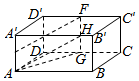 已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.
已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.
如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com