Question

7．某宾馆在装修时，为了美观，欲将客房的窗户设计成半径为1m的圆形，并用四根木条将圆分成如图所示的9个区域，其中四边形ABCD为中心在圆心的矩形，现计划将矩形ABCD区域设计为可推拉的窗口．
（1）若窗口ABCD为正方形，且面积大于$\frac{1}{4}$m²（木条宽度忽略不计），求四根木条总长的取值范围；
（2）若四根木条总长为6m，求窗口ABCD面积的最大值．

Answer 1

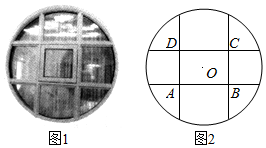
分析 （1）求出正方形的边长，可得正方形的面积，利用面积大于$\frac{1}{4}$m²，即可求四根木条总长的取值范围；
（2）设AB所在木条长为am，CD所在木条长为bm，求出AB，BD，可得窗口ABCD面积，利用基本不等式求窗口ABCD面积的最大值．

解答 解：（1）设一根木条长为xcm，则正方形的边长为2$\sqrt{1-（\frac{x}{2}）^{2}}$=$\sqrt{4-{x}^{2}}$，
∵S_ABCD＞$\frac{1}{4}$，
∴4-x²＞$\frac{1}{4}$，
∴x＜$\frac{\sqrt{15}}{2}$，
∵四根木条将圆分成9个区域，
∴x＞$\sqrt{2}$，
∴4$\sqrt{2}$＜4x＜2$\sqrt{15}$；
（2）设AB所在木条长为am，CD所在木条长为bm，
由条件，2a+2b=6，则a+b=3，
∵a，b∈（0，2），
∴b=3-a∈（0，2），∴a，b∈（1，2）．
∵AB=2$\sqrt{1-\frac{{b}^{2}}{4}}$，BD=2$\sqrt{1-\frac{{a}^{2}}{4}}$，
∴S_ABCD=4$\sqrt{1-\frac{{b}^{2}}{4}}$•$\sqrt{1-\frac{{a}^{2}}{4}}$=$\sqrt{4-{b}^{2}}$•$\sqrt{4-{a}^{2}}$≤$\frac{8-（{a}^{2}+{b}^{2}）}{2}$≤$\frac{8-\frac{（a+b）^{2}}{2}}{2}$=$\frac{7}{4}$，
当且仅当a=b=$\frac{3}{2}$∈（1，2）时，S_ABCD=$\frac{7}{4}$，
答：窗口ABCD面积的最大值为$\frac{7}{4}$．

点评 本题考查利用数学知识解决实际问题，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．