

| A. | 2010 | B. | 2009 | C. | 1006 | D. | 1005 |
分析 由已知,得出第n行的第一个数是n,该行共有2n-1个数字,且构成以1为公差的等差数列,根据等差数列前n项和公式,得出关于n的方程求出行数n即可.
解答 解:此图各行的数字排布规律是:第n行的第一个数是n,该行共有2n-1个数字,且构成以1为公差的等差数列.
所以第n行的各数之和为(2n-1)•n+$\frac{(2n-1)(2n-2)}{2}$=4n2-4n+1,
由4n2-4n+1=20112,得 4n(n-1)=20112-12=2012×2010=(2×1006)×(2×1005)=4×1006×1005
所以n=1006,
故选:C.
点评 本题考查等差数列前n项和公式的应用,得出图中各行数的排布规律是关键.考查抽象概括、计算能力.本题解关于n的方程时,对因式进行分解、对应.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=x g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=x g(x)=$\root{3}{{x}^{3}}$ | ||
| C. | f(x)=sinx g(x)=sin(π+x) | D. | f(x)=x g(x)=elnx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
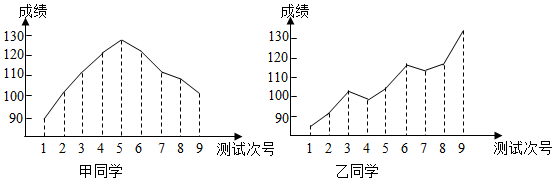
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e-1}{e}$ | B. | $\frac{2e-1}{e}$ | C. | $\frac{e-1}{2e}$ | D. | $\frac{2e-1}{2e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (0,3) | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
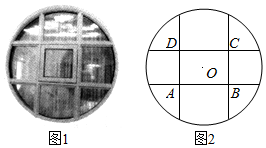
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com