
分析 (1)运用奇、偶函数的定义,由函数方程的思想可得f(x)、g(x)的解析式;
(Ⅱ)分别求出f(x),g(x)的导数,运用基本不等式和单调性可得最小值;
(Ⅲ)由题意可得当x>0时,$\frac{f(x)}{x}$>ag(x)+1-a?f(x)>axg(x)+(1-a)x,$\frac{f(x)}{x}$<bg(x)+1-b?f(x)<bxg(x)+(1-b)x,设函数h(x)=f(x)-cxg(x)-(1-c)x,通过导数判断单调性,即可得证.
解答 解:(Ⅰ)f(x)是奇函数,g(x)是偶函数,
即有f(-x)=-f(x),g(-x)=g(x),
f(x)+g(x)=2ex,f(-x)+g(-x)=2e-x,
即为-f(x)+g(x)=2e-x,
解得f(x)=ex-e-x,g(x)=ex+e-x;
(Ⅱ)当x≥0时,f′(x)=ex+e-x≥2$\sqrt{{e}^{x}•{e}^{-x}}$=2,
当且仅当x=0时,f(x)的切线的斜率取得最小值2;
g′(x)=ex-e-x在[0,+∞)递增,可得x=0时,
g(x)的切线的斜率取得最小值0;
(Ⅲ)证明:f′(x)=ex+e-x=g(x),
g′(x)=ex-e-x=f(x),
当x>0时,$\frac{f(x)}{x}$>ag(x)+1-a?f(x)>axg(x)+(1-a)x,
$\frac{f(x)}{x}$<bg(x)+1-b?f(x)<bxg(x)+(1-b)x,
设函数h(x)=f(x)-cxg(x)-(1-c)x,
h′(x)=f′(x)-c(g(x)+xg′(x))-(1-c)
=g(x)-cg(x)-cxf(x)-(1-c)=(1-c)(g(x)-1)-cxf(x),
①若c≤0则h′(x)>0,故h(x)在(0,+∞)递增,h(x)>h(0)=0,(x>0),
即有f(x)>cxg(x)+(1-c)x,故$\frac{f(x)}{x}$>ag(x)+1-a成立;
②若c≥1则h′(x)<0,故h(x)在(0,+∞)递减,h(x)<h(0)=0,(x>0),
即有f(x)<cxg(x)+(1-c)x,故$\frac{f(x)}{x}$<bg(x)+1-b成立.
综上可得,当x>0时,a g(x)+(1-a)<$\frac{f(x)}{x}$<b g(x)+(1-b),
即有当x>0时,曲线y=$\frac{f(x)}{x}$在曲线y=ag(x)+2(1-a)和y=bg(x)+2(1-b)之间,
且相互之间没有公共点.
点评 本题考查函数的奇偶性的运用,主要考查函数的解析式的求法和不等式的证明,同时考查指数函数的单调性和基本不等式的运用,以及导数的运用:判断单调性,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
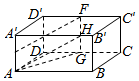 已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.
已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | C. | $\frac{1}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com