
分析 (1)求出g(x)的导数,由题意可得g′(x)≥0对x>0恒成立,即为a≥x-x2对x>0恒成立,求出右边函数的最大值,即可得到a的范围;
(2)(i)a=0时,求出g(x)的导数,可得切线的斜率,由两点的斜率公式,化简整理,结合中点坐标公式,即可得到结论;
(ii)当a≠0时,假设存在这样的A,B,使得g(x)在点Q(x0,g(x0))处的切线与直线AB平行.由两直线平行的条件:斜率相等,化简整理,结合中点坐标公式,化为ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$,设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),记函数h(t)=lnt-$\frac{2(t-1)}{t+1}$,求出导数,判断单调性,即可得到结论.
解答 解:(1)函数g(x)的定义域为(0,+∞),
g(x)的导数为g′(x)=$\frac{2a}{x}$+2x-2=$\frac{2({x}^{2}-x+a)}{x}$,
若函数g(x)在定义域上为单调增函数,可得g′(x)≥0对x>0恒成立,
即为a≥x-x2对x>0恒成立,
由h(x)=x-x2=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$,当x=$\frac{1}{2}$时,h(x)取得最大值$\frac{1}{4}$,
则a≥$\frac{1}{4}$;
(2)(i)a=0时,g(x)=x2-2x,g′(x)=2x-2,
g′(x0)=2x0-2,
设A(x1,g(x1)),B(x2,g(x2)),(0<x1<x2),
可得x0=$\frac{{x}_{1}+{x}_{2}}{2}$,
kAB=$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$=$\frac{({{x}_{1}}^{2}-2{x}_{1})-({{x}_{2}}^{2}-2{x}_{2})}{{x}_{1}-{x}_{2}}$
=$\frac{({x}_{1}+{x}_{2}-2)({x}_{1}-{x}_{2})}{{x}_{1}-{x}_{2}}$=x1+x2-2=2x0-2,
则g(x)在点Q(x0,g(x0))处的切线与直线AB平行;
(ii)当a≠0时,假设存在这样的A,B,
使得g(x)在点Q(x0,g(x0))处的切线与直线AB平行.
可得g′(x0)=$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$,
即$\frac{2a}{{x}_{0}}$+2x0-2=$\frac{(2aln{x}_{1}+{{x}_{1}}^{2}-2{x}_{1})-(2aln{x}_{2}+{{x}_{2}}^{2}-2{x}_{2})}{{x}_{1}-{x}_{2}}$,
由x0=$\frac{{x}_{1}+{x}_{2}}{2}$,可得$\frac{2a}{\frac{{x}_{1}+{x}_{2}}{2}}$+x1+x2-2=$\frac{2aln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$+x1+x2-2,
即ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$,设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),
记函数h(t)=lnt-$\frac{2(t-1)}{t+1}$,
则h′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$≥0,
可得h(t)在(0,1)递增,
可得当0<t<1时,h(t)<h(1)=0,
即方程lnt=$\frac{2(t-1)}{t+1}$在区间(0,1)上无解,
故不存在这样的A,B,使得g(x)在点Q(x0,g(x0))处的切线与直线AB平行.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式恒成立问题的解法,以及两直线平行的条件:斜率相等,考查化简整理和构造函数的能力,属于难题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $x>-\frac{2}{3}$ | B. | $x>-\frac{3}{2}$ | C. | $x<-\frac{2}{3}$ | D. | $x<-\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
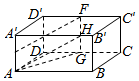 已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.
已知长方体ABCD-A1B1C1D1,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,E,F分别为AA1,C1D1中点,则$\overrightarrow{EF}$可用$\vec a,\vec b,\vec c$表示为$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$)+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.
如图,四棱锥O-ABCD中,AC垂直平分BD,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OD}$|=1,则($\overrightarrow{OA}$+$\overrightarrow{OC}$)•($\overrightarrow{OB}$-$\overrightarrow{OD}$)的值是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com