
 如图,某市园林局准备绿化一块直径为BC的半圆形空地,△ABC以外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a(a为定值),∠ABC=α,设△ABC的面积为S1,正方形PQRS的面积为S2;
如图,某市园林局准备绿化一块直径为BC的半圆形空地,△ABC以外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a(a为定值),∠ABC=α,设△ABC的面积为S1,正方形PQRS的面积为S2;分析 (1)在Rt△ABC中,BC=a,∠ABC=α,由AB=acosα,AC=asinα,能求出S1;设正方形PQRS的边长为x,则BP=$\frac{x}{sinα}$,AP=xcosα,由BP+AP=$\frac{x}{sinα}+xcosα$,AB=acosα,AP+BP=AB,能求出S2.
(2)$\frac{{S}_{2}}{{S}_{1}}$=$\frac{4sin2α}{4+si{n}^{2}2α+4sin2α}$,令sin2α=t,推导出$\frac{{S}_{2}}{{S}_{1}}$=$\frac{4}{t+\frac{4}{t}+4}$,0<t≤1,设f(t)=t+$\frac{4}{t}+4$(0<t≤1),推导出f(t)=t+$\frac{4}{t}$+4在(0,1]上单调递减,由此能求出$\frac{{s}_{2}}{{s}_{1}}$的最大值及相应的α.
解答 解:(1)在Rt△ABC中,BC=a,∠ABC=α,
∴AB=acosα,AC=asinα,
∴S1=$\frac{1}{2}{a}^{2}sinαcosα$=$\frac{1}{4}{a}^{2}sin2α$,
设正方形PQRS的边长为x,则BP=$\frac{x}{sinα}$,AP=xcosα,
由BP+AP=$\frac{x}{sinα}+xcosα$,AB=acosα,又AP+BP=AB,
∴x=$\frac{αsinαcosα}{1+sinαcosα}$=$\frac{asin2α}{2+sin2α}$,
∴S2=x2=($\frac{asin2α}{2+sin2α}$)2=$\frac{{a}^{2}si{n}^{2}2α}{4+si{n}^{2}2α+4sin2α}$.
(2)$\frac{{S}_{2}}{{S}_{1}}$=$\frac{\frac{{a}^{2}si{n}^{2}2α}{1+si{n}^{2}2α+4sin2α}}{\frac{1}{4}{a}^{2}sin2α}$
=$\frac{4sin2α}{4+si{n}^{2}2α+4sin2α}$,
令sin2α=t,由0<α<$\frac{π}{2}$,得0<2α<π,∴0<t≤1.
∴$\frac{{S}_{2}}{{S}_{1}}$=$\frac{4t}{4+{t}^{2}+4t}$=$\frac{4}{t+\frac{4}{t}+4}$,0<t≤1,
设f(t)=t+$\frac{4}{t}+4$(0<t≤1),任取0<t1<t1≤1,
则f(t1)-f(t2)=${t}_{1}+\frac{4}{{t}_{1}}$-${t}^{2}-\frac{4}{{t}^{2}}$=(t1-t2),$\frac{({t}_{1}{t}_{2}-4)}{{t}_{1}{t}_{2}}$>0,
∴f(t)=t+$\frac{4}{t}$+4在(0,1]上单调递减,∴f(t)≥9,
∴0<$\frac{4}{t+\frac{4}{t}+4}$≤$\frac{4}{9}$,
∴$\frac{{s}_{2}}{{s}_{1}}$的最大值为$\frac{4}{9}$,此时α=$\frac{π}{4}$.
点评 本题考查三角形面积、正方形面积的求法,考查三角形面积、正方形面积比值的最大值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | p2,p3 | B. | p2,p4 | C. | p1,p3 | D. | p1,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
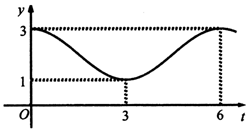 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 水上狂欢节编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 16 | B. | $\frac{4}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com