解:(1)由函数f(x)=x
2-(a+2)x+alnx(常数a>2)可知:其定义域为(0,+∞).

∴
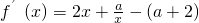
=
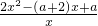
=
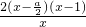
,
令f
′(x)=0,解得
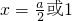
,
∵a>2,∴

.
列表如图:
由表格可知:当x=1时,函数f(x)取得极大值,且f(1)=-a-1;当x=

时,函数f(x)取得极小值,且
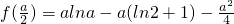
.
(2)当a=4时,函数f(x)=x
2-6x+4lnx存在“类对称点”,为点P
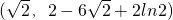
.
当a=4时,f(x)=x
2-6x+4lnx,∴f
′(x)=2x-6
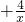
,
设切点P(m,f(m)),则切线的斜率为f
′(m)=
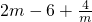
,
则切线的方程为y-f(m)=f
′(m)(x-m),
由
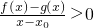
在(0,+∞)上恒成立?
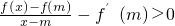
在(0,+∞)恒成立.(*)
其中
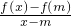
为过点(x,f(x))、(m,f(m))的割线的斜率,而f
′(m)为过切点P(m,f(m))的切线的斜率.

要使(*)式恒成立,f
′(x)必取得最小值.
∵[f
′(x)]
′=2
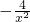
=
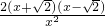
,令f
″(x)=0,解得x=

.
由表格可知:当且仅当x=

时,f
′(x)取得极小值,也是最小值.
即当x=

时,
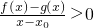
在(0,+∞)上恒成立.
故
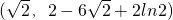
是函数f(x)的一个“类对称点”.
分析:(1)先求出导数f
′(x)=0时的x的值,再判断是否是极值点,若是即可求出极值;
(2)利用“类对称点”的定义,证明
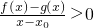
在(0,+∞)上恒成立?
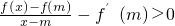
在(0,+∞)恒成立即可.
点评:熟练掌握利用导数研究函数的单调性和极值的方法及正确理解“类对称点”的意义是解题的关键.

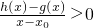 在D内恒成立,则称P为函数y=h(x)的“类对称点”,当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
在D内恒成立,则称P为函数y=h(x)的“类对称点”,当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
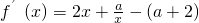 =
=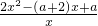 =
=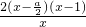 ,
,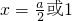 ,
, .
. 时,函数f(x)取得极小值,且
时,函数f(x)取得极小值,且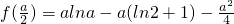 .
.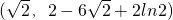 .
.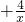 ,
,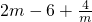 ,
,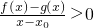 在(0,+∞)上恒成立?
在(0,+∞)上恒成立?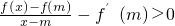 在(0,+∞)恒成立.(*)
在(0,+∞)恒成立.(*)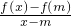 为过点(x,f(x))、(m,f(m))的割线的斜率,而f′(m)为过切点P(m,f(m))的切线的斜率.
为过点(x,f(x))、(m,f(m))的割线的斜率,而f′(m)为过切点P(m,f(m))的切线的斜率.
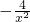 =
=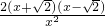 ,令f″(x)=0,解得x=
,令f″(x)=0,解得x= .
. 时,f′(x)取得极小值,也是最小值.
时,f′(x)取得极小值,也是最小值. 时,
时,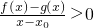 在(0,+∞)上恒成立.
在(0,+∞)上恒成立.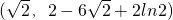 是函数f(x)的一个“类对称点”.
是函数f(x)的一个“类对称点”.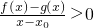 在(0,+∞)上恒成立?
在(0,+∞)上恒成立?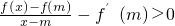 在(0,+∞)恒成立即可.
在(0,+∞)恒成立即可.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<