
分析 对于命题p:x2+x+4≥mx对一切的x<0恒成立,即$m≥x+\frac{4}{x}+6$对一切的x<0恒成立,变形利用基本不等式的性质即可得出.关于x的一元二次方程x2+(m-3)x+m+5=0的实数根均是正数,可得$\left\{{\begin{array}{l}{△={{({m-3})}^2}-4({m+5})≥0}\\{{x_1}+{x_2}=3-m>0}\\{{x_1}•{x_2}=m+5>0}\end{array}}\right.$.再利用“p∨q”为真,“p∧q”为假,即可得出.
解答 解:∵x2+x+4≥mx对一切的x<0恒成立,即$m≥x+\frac{4}{x}+6$对一切的x<0恒成立,
又∵$x+\frac{4}{x}+1=-[{({-x})+({-\frac{4}{x}})}]+1≤-2\sqrt{({-x})({-\frac{4}{x}})}+6=-3$,当且仅当$-x=-\frac{4}{x}$即x=-2时,取等号,
∴p为真,则m≥-3.
∵关于x的一元二次方程x2+(m-3)x+m+5=0的实数根均是正数,
∴$\left\{{\begin{array}{l}{△={{({m-3})}^2}-4({m+5})≥0}\\{{x_1}+{x_2}=3-m>0}\\{{x_1}•{x_2}=m+5>0}\end{array}}\right.$解得-5<m≤-1.
∴q为真,则-5<m≤-1.
∵p∨q”为真,“p∧q”为假,
∴p真q假或p假q真,
∴$\left\{{\begin{array}{l}{m≥-3}\\{m≤-5或m>-1}\end{array}}\right.$,或$\left\{{\begin{array}{l}{m<-3}\\{-5<m≤-1}\end{array}}\right.$,
∴m>-1或-5<m<-3.
点评 本题考查了基本不等式的性质、一元二次方程的实数根与判别式根与系数的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
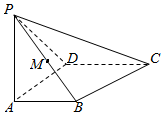 四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.
四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
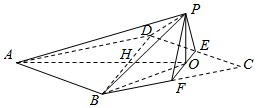 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com