解:(Ⅰ)∵点(a
n+1,S
n)在直线2x+y-2=0上,∴2a
n+1 +S
n -2=0. ①
n≥2时,2a
n+s
n-1-2=0. ②
①─②得 2a
n+1 -2a
n+a
n=0,∴

=

(n≥2).
再由a
1=1,可得 a
2=

.
∴{a
n}是首项为1,公比为

的等比数列,
∴a
n =

.
(Ⅱ)由(Ⅰ)可得 s
n=
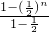
=2-

.
若数列{S
n+λ•n+
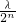
}为等差数列,
则 s
1+λ+

,s
2+2λ+

,s
3+3λ+
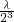
成等差数列,
∴2(s
2+2λ+

)=(s
1+λ+

)+(s
3+3λ+
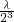
),解得 λ=2.
又λ=2时,S
n+λ•n+
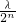
=2n+2,显然 {2n+2}成等差数列,
故存在实数λ=2,使得数列 {S
n+λ•n+
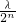
}成等差数列.
分析:(Ⅰ)由已知条件可得 2a
n+1 +S
n -2=0,可得n≥2时,2a
n+s
n-1-2=0,相减可得

=

(n≥2).由此可得{a
n}是首项为1,公比为

的等比数列,由此求得数列{a
n}的通项公式.
(Ⅱ)先求出s
n=2-

,若数列{S
n+λ•n+
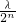
}为等差数列,则由第二项的2倍等于第一项加上第三项,求出λ=2,经检验λ=2时,此数列的通项公式是关于n的一次函数,故满足数列为等差数列,从而得出结论.
点评:本题主要考查等差关系的确定,根据数列的递推关系求通项,属于中档题.

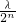 }为等差数列?若存在,求出λ的值;若不存在,则说明理由.
}为等差数列?若存在,求出λ的值;若不存在,则说明理由. =
= (n≥2).
(n≥2). .
. 的等比数列,
的等比数列, .
.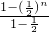 =2-
=2- .
.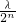 }为等差数列,
}为等差数列, ,s2+2λ+
,s2+2λ+ ,s3+3λ+
,s3+3λ+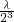 成等差数列,
成等差数列, )=(s1+λ+
)=(s1+λ+ )+(s3+3λ+
)+(s3+3λ+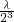 ),解得 λ=2.
),解得 λ=2. 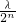 =2n+2,显然 {2n+2}成等差数列,
=2n+2,显然 {2n+2}成等差数列,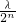 }成等差数列.
}成等差数列. =
= (n≥2).由此可得{an}是首项为1,公比为
(n≥2).由此可得{an}是首项为1,公比为 的等比数列,由此求得数列{an}的通项公式.
的等比数列,由此求得数列{an}的通项公式. ,若数列{Sn+λ•n+
,若数列{Sn+λ•n+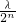 }为等差数列,则由第二项的2倍等于第一项加上第三项,求出λ=2,经检验λ=2时,此数列的通项公式是关于n的一次函数,故满足数列为等差数列,从而得出结论.
}为等差数列,则由第二项的2倍等于第一项加上第三项,求出λ=2,经检验λ=2时,此数列的通项公式是关于n的一次函数,故满足数列为等差数列,从而得出结论.
