
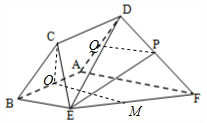
 ��ͼ����֪����ABCD��ֱ������ABEF���ڵ�ƽ�滥�ഹֱ������BE��AF��AB��AF��AB=BE=$\frac{1}{2}$AF=2����CBA=$\frac{��}{3}$��PΪDF���е㣮
��ͼ����֪����ABCD��ֱ������ABEF���ڵ�ƽ�滥�ഹֱ������BE��AF��AB��AF��AB=BE=$\frac{1}{2}$AF=2����CBA=$\frac{��}{3}$��PΪDF���е㣮���� ����ȡAD���е�Q������PQ��BQ��֤��PE��BQ������֤��PE��ƽ��ABCD��
����ȡAB�е�O������CO���ֱ���OB��OM��OC����ֱ��Ϊx��y��z�Ὠ���ռ�ֱ������ϵ�����ƽ��DEF�ķ�������ƽ��AEF�ķ������������������������������D-EF-A������ֵ��
�������$\overrightarrow{FG}=��-�ˣ�-4��\sqrt{3}�ˣ�$��ƽ��ABEF�ķ���������ֱ��FG��ƽ��ABEF���ɽ�Ϊ�ȣ������������г�������⼴�ɣ�
���  ����С������13�֣�
����С������13�֣�
�⣺����ȡAD���е�Q������PQ��BQ����PQ��AF��BE����$PQ=\frac{1}{2}AF=BE$��
�����ı���BEPQΪƽ���ı��Σ�����2�֣�
����PE��BQ����BQ?ƽ��ABCD��PE?ƽ��ABCD��
��PE��ƽ��ABCD������3�֣�
����ȡAB�е�O������CO����CO��AB����Ϊƽ��ABCD��ƽ��ABEF������ΪAB��
��CO��ƽ��ABEF����4�֣�
��OM��AF���ֱ���OB��OM��OC����ֱ��Ϊx��y��z�Ὠ���ռ�ֱ������ϵ��
��$D��-2��0��\sqrt{3}����F��-1��4��0����E��1��2��0��$����5�֣�
����$\overrightarrow{DF}=��1��4��-\sqrt{3}��\overrightarrow{��EF}=��-2��2��0��$����ƽ��DEF�ķ�����$\overrightarrow m=��x��y��z��$��
��$\left\{\begin{array}{l}x+4y-\sqrt{3}z=0\\-2x+2y=0\end{array}\right.$��x=1����$y=1��z=\frac{5}{{\sqrt{3}}}$����6�֣�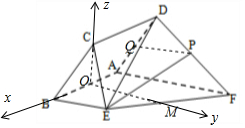
ƽ��AEF�ķ�����$\overrightarrow n=��0��0��1��$����7�֣�
����$cos\left?{\overrightarrow m��\overrightarrow n}\right��=\frac{{\frac{5}{{\sqrt{3}}}}}{{\sqrt{\frac{31}{3}}}}=\frac{{5\sqrt{31}}}{31}$����8�֣�
����Ϊ�����D-EF-AΪ��ǣ�����������ֵΪ$\frac{{5\sqrt{31}}}{31}$�� ����9�֣�
����$A��-1��0��0����\overrightarrow{AD}=��-1��0��\sqrt{3}����\overrightarrow{AG}=��-�ˣ�0��\sqrt{3}�ˣ�$����$G��-��-1��0��\sqrt{3}�ˣ�$��$\overrightarrow{FG}=��-�ˣ�-4��\sqrt{3}�ˣ�$����ƽ��ABEF�ķ�����Ϊ$\overrightarrow m=��0��0��1��$��
��ֱ��FG��ƽ��ABEF���ɽ�Ϊ�ȣ�
����$sin��=\frac{{\sqrt{3}��}}{{\sqrt{16+4{��^2}}}}=\frac{{\sqrt{39}}}{26}$����11�֣�
����$��=\frac{{\sqrt{3}}}{3}$��$AG=\frac{{2\sqrt{3}}}{3}$������13�֣�
���� ���⿼�����ǵ�ƽ��ǵ���ֱ����ƽ���г��۵���ֱ����ƽ��ƽ�е��жϣ�����ռ����������Լ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | �ܼ� | |
| �װ� | 10 | 45 | 55 |
| �Ұ� | 20 | 30 | 55 |
| �ϼ� | 30 | 75 | 105 |
| p��K2��k�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2��}{9}$ | B�� | $\frac{��}{9}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ң��� | B�� | �ף��� | C�� | �ף��� | D�� | �ң��� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com