
分析 (1)法一:根据绝对值的性质求出f(x)的最小值,得到x=$\frac{b}{2}$时取等号,证明结论即可;法二:根据f(x)的分段函数的形式,求出f(x)的最小值,证明即可;
(2)法一,二:问题转化为$\frac{a+2b}{ab}$≥t恒成立,根据基本不等式的性质求出$\frac{a+2b}{ab}$的最小值,从而求出t的范围即可;法三:根据二次函数的性质判断即可.
解答 解:(1)法一:f(x)=|x+a|+|2x-b|=|x+a|+|x-$\frac{b}{2}$|+|x-$\frac{b}{2}$|,
∵|x+a|+|x-$\frac{b}{2}$|≥|(x+a)-(x-$\frac{b}{2}$)|=a+$\frac{b}{2}$且|x-$\frac{b}{2}$|≥0,
∴f(x)≥a+$\frac{b}{2}$,当x=$\frac{b}{2}$时取等号,即f(x)的最小值为a+$\frac{b}{2}$,
∴a+$\frac{b}{2}$=1,2a+b=2;
法二:∵-a<$\frac{b}{2}$,∴f(x)=|x+a|+|2x-b|=$\left\{\begin{array}{l}{-3x-a+b,x<-a}\\{-x+a+b,-a≤x<\frac{b}{2}}\\{3x+a-b,x≥\frac{b}{2}}\end{array}\right.$,
显然f(x)在(-∞,$\frac{b}{2}$]上单调递减,f(x)在[$\frac{b}{2}$,+∞)上单调递增,
∴f(x)的最小值为f($\frac{b}{2}$)=a+$\frac{b}{2}$,
∴a+$\frac{b}{2}$=1,2a+b=2.
(2)方法一:∵a+2b≥tab恒成立,∴$\frac{a+2b}{ab}$≥t恒成立,
$\frac{a+2b}{ab}$=$\frac{1}{b}$+$\frac{2}{a}$=($\frac{1}{b}$+$\frac{2}{a}$)(2a+b )•$\frac{1}{2}$=$\frac{1}{2}$(1+4+$\frac{2a}{b}$+$\frac{2b}{a}$)$≥\frac{1}{2}(1+4+2\sqrt{\frac{2a}{b}•\frac{2b}{a}})=\frac{9}{2}$,
当a=b=$\frac{2}{3}$时,$\frac{a+2b}{ab}$取得最小值$\frac{9}{2}$,
∴$\frac{9}{2}$≥t,即实数t的最大值为$\frac{9}{2}$;
方法二:∵a+2b≥tab恒成立,
∴$\frac{a+2b}{ab}$≥t恒成立,
t≤$\frac{a+2b}{ab}$=$\frac{1}{b}$+$\frac{2}{a}$恒成立,
$\frac{1}{b}$+$\frac{2}{a}$=$\frac{1}{b}$+$\frac{4}{2a}$≥$\frac{{(1+2)}^{2}}{b+2a}$=$\frac{9}{2}$,
∴$\frac{9}{2}$≥t,即实数t的最大值为$\frac{9}{2}$;
方法三:∵a+2b≥tab恒成立,
∴a+2(2-a)≥ta(2-a)恒成立,
∴2ta2-(3+2t)a+4≥0恒成立,
∴(3+2t)2-326≤0,
∴$\frac{1}{2}$≤t≤$\frac{9}{2}$,实数t的最大值为$\frac{9}{2}$.
点评 本题考查了绝对值不等式问题,考查绝对值的性质以及二次函数的性质,考查转化思想,是一道中档题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:填空题
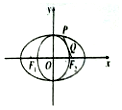 如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.
如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
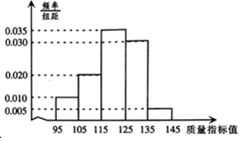 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $6\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$π | B. | $\frac{27\sqrt{3}π}{2}$ | C. | 27π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com