
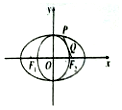
 如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$.
如图,F1,F2是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右两焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q是线段PF2的中点,则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$(e为椭圆的离心率)的最小值为$\frac{\sqrt{5}}{3}$. 分析 连接PF1,OQ,运用中位线定理可得|F1P|=2|OQ|=2b,由椭圆的定义可得|PF1|+|PF2|=2a,可得|PF2|=2a-2b,运用勾股定理,化简可得3b=2a,e=$\frac{\sqrt{5}}{3}$,求得${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$=$\frac{1}{2}$(a+$\frac{5}{9a}$),运用基本不等式即可得到最小值.
解答 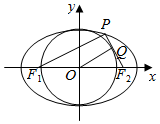 解:连接F1P,OQ,因为点Q为线段PF2的中点,所以|F1P|=2|OQ|=2b,
解:连接F1P,OQ,因为点Q为线段PF2的中点,所以|F1P|=2|OQ|=2b,
由椭圆的定义得|PF2|=2a-2b,由F1P⊥F2P,得(2b)2+(2a-2b)2=(2c)2,解得2a=3b,e=$\frac{\sqrt{5}}{3}$,
所以${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$=$\frac{1}{2}$(a+$\frac{5}{9a}$)≥$\frac{1}{2}$•2$\sqrt{a•\frac{5}{9a}}$=$\frac{\sqrt{5}}{3}$(当且仅当a=$\frac{\sqrt{5}}{3}$时等号成立).
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查最值的求法,注意运用椭圆的定义和基本不等式,考查圆的切线的性质的运用,以及中位线定理和勾股定理,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | -4 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | 2或$\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 55 |
| 合计 | 30 | 75 | 105 |
| p(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com