练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知$\overrightarrow{e_1}，\overrightarrow{e_2}$为平面内两个不共线向量，$\overrightarrow{MN}=2\overrightarrow{e_1}-3\overrightarrow{e_2}\;，\;\overrightarrow{NP}=λ\overrightarrow{e_1}+6\overrightarrow{e_2}$，若M、N、P三点共线，
    则λ=（　　）
    A．-9B．-4C．4D．9

    分析 利用向量共线定理、共面向量基本定理即可得出．

    解答 解：∵M、N、P三点共线，∴存在实数k使得$\overrightarrow{MN}$=k$\overrightarrow{NP}$，
    ∴$2\overrightarrow{{e}_{1}}-3\overrightarrow{{e}_{2}}$=k$（λ\overrightarrow{{e}_{1}}+6\overrightarrow{{e}_{2}}）$，又$\overrightarrow{e_1}，\overrightarrow{e_2}$为平面内两个不共线向量，
    可得2=kλ，-3=6k，
    解得λ=-4．
    故选：B．

    点评 本题考查了向量共线定理、共面向量基本定理，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知直线l：x-$\sqrt{3}$y+2=0与圆x2+y2=4交于A，B两点，则$\overrightarrow{AB}$在x轴正方向上投影的绝对值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．求下列函数定义域（结果用集合或区间表示）：
    （1）$y=\frac{{\sqrt{x-4}}}{|x|-5}$
    （2）y=loga（2-x）（a＞0且a≠1）
    （3）$y=\sqrt{1-{{（{\frac{1}{2}}）}^x}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在△ABC中，AB=3，AC=2，A=60°，则S△ABC=$\frac{3}{2}$$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．点P是曲线y=x2上任意一点，则点P到直线y=2x-2的最小距离为$\frac{\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．对于△ABC，有如下四个命题：
    ①若sin2A=sin2B，则△ABC为等腰三角形；
    ②若sinB=cosA，则△ABC是直角三角形；
    ③若sin2A+sin2B＞sin2C，则△ABC是锐角三角形；
    ④若$\frac{a}{cosA}=\frac{b}{cosB}=\frac{c}{cosC}$，则△ABC是等边三角形．
    其中正确的项有④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

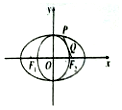    6．如图，F1，F2是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右两焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q是线段PF2的中点，则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$（e为椭圆的离心率）的最小值为$\frac{\sqrt{5}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．由曲线y=x2与直线y=x+2所围成的平面图形的面积为$\frac{9}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

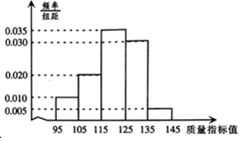    4．从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图，则这500件产品质量指标值的样本方差s2是110（同一组中的数据用该组区间的中点值作代表）

    查看答案和解析>>

    同步练习册答案