
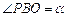 ,求y
,求y 关于
关于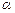 的函数关系式;
的函数关系式; 区的距离之和最小?
区的距离之和最小?
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源:不详 题型:单选题
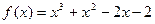 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:| f(1)=-2 | f(1.5)=0.625 | f(1.25)=-0.984 |
| f(1.375)=-0.260 | f(1.4375)=0.162 | f(1.40625)=-0.054 |
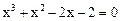 的一个近似根(精确到0.1)为( ).
的一个近似根(精确到0.1)为( ).| A.1.4 | B.1.3 | C.1.2 | D.1.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
,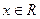 ,有下列4个命题:
,有下列4个命题: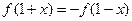 ,则
,则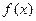 的图象自身关于点
的图象自身关于点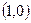 对称;
对称;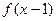 与
与 的图象关于直线
的图象关于直线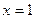 对称;
对称;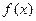 为偶函数,且
为偶函数,且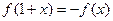 ,则
,则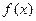 的图象自身关于直线
的图象自身关于直线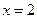 对称;
对称;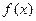 为奇函数,且
为奇函数,且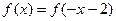 ,则
,则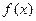 的图象自身关于直线
的图象自身关于直线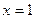 对称;
对称;| A.①③④ | B.②④ | C.①②③ | D.①②③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com