
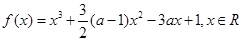 .
. 的单调区间;
的单调区间;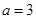 时,若函数
时,若函数 在区间
在区间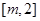 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.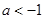 时,
时, 在
在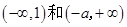 内单调递增,
内单调递增, 在
在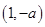 内单调递减;当
内单调递减;当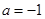 时,
时, 在
在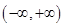 单调递增;当
单调递增;当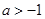 时,
时, 在
在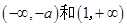 内单调递增,
内单调递增, 在
在 内单调递减;(Ⅱ)即
内单调递减;(Ⅱ)即 的取值范围是
的取值范围是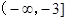 .
. 的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出
的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出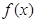 的导函数,判断
的导函数,判断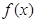 的导函数的符号,从而求出
的导函数的符号,从而求出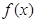 的单调区间;但本题求导后令
的单调区间;但本题求导后令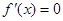 ,得
,得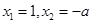 ,由于不知
,由于不知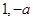 的大小,因此需要对
的大小,因此需要对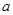 进行分类讨论,从而确定在各种情况下的单调区间;(Ⅱ)当
进行分类讨论,从而确定在各种情况下的单调区间;(Ⅱ)当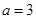 时,若函数
时,若函数 在区间
在区间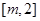 上的最大值为28,求
上的最大值为28,求 的取值范围,这是函数在闭区间上的最值问题,像这一类问题的处理方法为,先求出
的取值范围,这是函数在闭区间上的最值问题,像这一类问题的处理方法为,先求出 的极值点,然后分别求出极值点与区间端点处的函数值,比较谁大谁为最大值,比较谁小谁为最小值,但本题是给出最大值,确定区间端点的取值范围,只需找出包含最大值28的
的极值点,然后分别求出极值点与区间端点处的函数值,比较谁大谁为最大值,比较谁小谁为最小值,但本题是给出最大值,确定区间端点的取值范围,只需找出包含最大值28的 的取值范围,
的取值范围,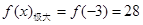 ,故故区间
,故故区间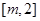 内必须含有
内必须含有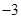 ,即
,即 的取值范围是
的取值范围是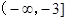 .
.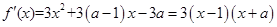 ,令
,令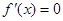 得
得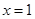 ,
,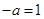 ,即
,即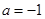 时,
时, ,
, 在
在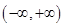 单调递增,
单调递增,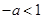 ,即
,即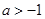 时,当
时,当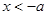 ,或
,或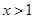 时,
时,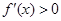 ,
, 在
在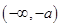 、
、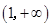 内单调递增,当
内单调递增,当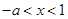 时
时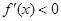 ,
, 在
在 内单调递减,
内单调递减,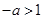 ,即
,即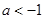 时,当
时,当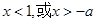 时
时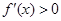 ,
, 在
在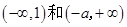 内单调递增
内单调递增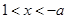 时
时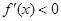 ,
, 在
在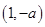 内单调递减 ,
内单调递减 ,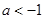 时,
时, 在
在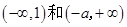 内单调递增,
内单调递增, 在
在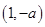 内单调递减;当
内单调递减;当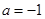 时,
时, 在
在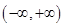 单调递增;当
单调递增;当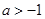 时,
时, 在
在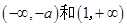 内单调递增,
内单调递增, 在
在 内单调递减;
内单调递减;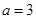 时,
时,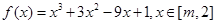 ,
,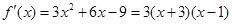 ,令
,令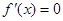 得
得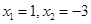 ,将
,将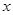 ,
,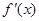 ,
, 变化情况列表如下:
变化情况列表如下: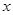 | 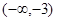 | 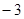 | 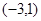 | 1 | 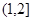 |
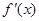 | 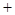 | 0 | 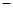 | 0 | 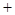 |
 | ↗ | 极大 | ↘ | 极小 | ↗ |
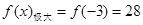 ,
,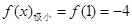 ,
,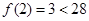 ,故区间
,故区间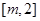 内必须含有
内必须含有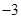 ,即
,即 的取值范围是
的取值范围是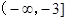 .
.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com