
已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2,若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )
A.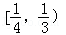 | B.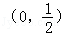 |
C.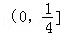 | D.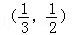 |
C
解析试题分析:根据f(x+1)=﹣f(x),可得f(x)是周期为2的周期函数. 再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,可得函数在[﹣1,3]上的解析式.根据题意可得
函数y=f(x)的图象与直线y="kx+k" 有4个交点,数形结合可得实数k的取值范围.
∵函数f(x)满足f(x+1)=﹣f(x),故有f(x+2)=f(x),故f(x)是周期为2的周期函数.再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,
可得当x∈[﹣1,0]时,f(x)=x2,故当x∈[﹣1,1]时,f(x)=x2,当x∈[1,3]时,f(x)=(x﹣2)2.
由于函数g(x)=f(x)﹣kx﹣k有4个零点,故函数y=f(x)的图象与直线y="kx+k" 有4个交点,如图所示:
把点(3,1)代入y=kx+k,可得k=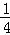 ,数形结合可得实数k的取值范围是 (0,
,数形结合可得实数k的取值范围是 (0,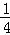 ],
],
故选C.
考点:根的存在性及根的个数判断
点评:本题主要考查函数的周期性的应用,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com