
| A. | $(1,-\frac{π}{4})$ | B. | $(1,\frac{3π}{4})$ | C. | $(\sqrt{2},-\frac{π}{4})$ | D. | $(\sqrt{2},\frac{3π}{4})$ |
分析 圆C的方程为ρ=2cos(θ+$\frac{π}{4}$),即ρ2=2ρcos(θ+$\frac{π}{4}$),展开为:ρ2=2×$\frac{\sqrt{2}}{2}$(ρcosθ-ρsinθ),把ρ2=x2+y2,x=ρcosθ,y=ρsinθ代入即可得出直角坐标方程,配方可得圆心直角坐标,化为极坐标即可得出.
解答 解:圆C的方程为ρ=2cos(θ+$\frac{π}{4}$),即ρ2=2ρcos(θ+$\frac{π}{4}$),
展开为:ρ2=2×$\frac{\sqrt{2}}{2}$(ρcosθ-ρsinθ),
∴直角坐标方程为:x2+y2=$\sqrt{2}x$-$\sqrt{2}$y.
配方为:$(x-\frac{\sqrt{2}}{2})^{2}+(y+\frac{\sqrt{2}}{2})^{2}$=1,
圆心为C$(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$.
∴$ρ=\sqrt{(\frac{\sqrt{2}}{2})^{2}×2}$=1,tanθ=-1,θ∈$(-\frac{π}{2},0)$,解得$θ=-\frac{π}{4}$.
∴C的极坐标为:$(1,-\frac{π}{4})$.
故选:A.
点评 本题考查了极坐标方程化为直角坐标方程的方法,考查了推理能力与计算能力,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中点,AC,BD交于O点,求二面角Q-BD-C的大小.
在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中点,AC,BD交于O点,求二面角Q-BD-C的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | k1+k2=k3 | B. | k1=k2=k3 | C. | k1+k2>k3 | D. | k1+k2<k3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,以矩形ABCD的一边AB为直径的半圆与对边CD相切,E为BC的中点,P为半圆弧上任意一点.若$\overrightarrow{AP}$=λ$\overrightarrow{AD}$+μ$\overrightarrow{AE}$,则λ-μ的最大值为( )
如图,以矩形ABCD的一边AB为直径的半圆与对边CD相切,E为BC的中点,P为半圆弧上任意一点.若$\overrightarrow{AP}$=λ$\overrightarrow{AD}$+μ$\overrightarrow{AE}$,则λ-μ的最大值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
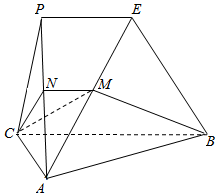 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP,AE分别于点N,M,设$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP,AE分别于点N,M,设$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com