
【题目】已知直线l的参数方程为 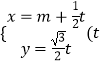 为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为
为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为 ![]() ,且直线l经过椭圆C的右焦点F.
,且直线l经过椭圆C的右焦点F.
(1)求椭圆C的内接矩形PMNQ面积的最大值;
(2)若直线l与椭圆C交于A,B两点,求|FA||FB|的值.
【答案】
(1)解:椭圆C化为5ρ2cos2θ+9ρ2sin2θ=45,∴5x2+9y2=45,
∴椭圆的标准方程: ![]() .设椭圆C的内接矩形PMNQ中,P的坐标为
.设椭圆C的内接矩形PMNQ中,P的坐标为 ![]() ,
,
∴ ![]() .
.
∴椭圆C的内接矩形PMNQ面积最大值为 ![]()
(2)解:由椭圆C的方程 ![]() ,得椭圆C的右焦点F(2,0),由直线l经过右焦点F(2,0),得m=2,
,得椭圆C的右焦点F(2,0),由直线l经过右焦点F(2,0),得m=2,
易得直线l的参数方程可化为 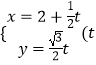 为参数),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
为参数),代入到5x2+9y2=45,整理得,8t2+10t﹣25=0,
∴ ![]() ,即
,即 ![]() .
.
|FA||FB|的值 ![]()
【解析】(1)将椭圆的极坐标方程转化成标准方程,设P点坐标,根据二倍角公式及正弦函数的性质,即可求得椭圆C的内接矩形PMNQ面积的最大值;(2)将参数方程代入椭圆的标准方程,由韦达定理即可求得 ![]() ,即可求得|FA||FB|的值.
,即可求得|FA||FB|的值.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足 ![]() =logabn(n∈N*),求数列{(an+6)bn}的前n项和.
=logabn(n∈N*),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某店销售进价为2元/件的产品![]() ,该店产品
,该店产品![]() 每日的销售量
每日的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)满足关系式
(单位:元/件)满足关系式![]() ,其中
,其中![]() .
.
(1)若产品![]() 销售价格为4元/件,求该店每日销售产品
销售价格为4元/件,求该店每日销售产品![]() 所获得的利润;
所获得的利润;
(2)试确定产品![]() 的销售价格,使该店每日销售产品
的销售价格,使该店每日销售产品![]() 所获得的利润最大.(保留1位小数)
所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 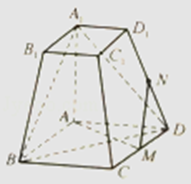
(1)求证:AM⊥A1B;
(2)若M为CD的中点,N为棱DD1上的点,且MN与平面A1BD所成角的正弦值为 ![]() ,试求DN的长.
,试求DN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥的轴截面SAB是边长为2的等边三角形,O为底面中心,M为SO的中点,动点P在圆锥底面内(包括圆周).若AM⊥MP,则P点形成的轨迹的长度为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
A.该金锤中间一尺重3斤
B.中间三尺的重量和是头尾两尺重量和的3倍
C.该金锤的重量为15斤
D.该金锤相邻两尺的重量之差的绝对值为0.5斤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com