
【题目】在数列{an}中,a1=4,nan+1﹣(n+1)an=2n2+2n.
(Ⅰ)求证:数列 ![]() 是等差数列;
是等差数列;
(Ⅱ)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
【答案】解:(I)解法一:(Ⅰ) ![]() 的两边同时除以n(n+1), 得
的两边同时除以n(n+1), 得 ![]() ,(3分)
,(3分)
所以数列 ![]() 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
解法二:依题意,可得 ![]() ,
,
所以 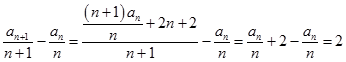 ,
,
即 ![]() ,
,
所以数列 ![]() 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(Ⅱ)由(Ⅰ),得 ![]() ,(7分)
,(7分)
所以 ![]() ,故
,故 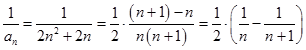 ,
,
所以 ![]()
= ![]()
= ![]()
【解析】(I)解法一: ![]() 的两边同时除以n(n+1),
的两边同时除以n(n+1), ![]() ,即可证明解法二:依题意,可得
,即可证明解法二:依题意,可得 ![]() ,可得
,可得 ![]() ,即可证明.(Ⅱ)由(Ⅰ),得
,即可证明.(Ⅱ)由(Ⅰ),得 ![]() ,可得
,可得 ![]() ,
, ![]() =
= ![]() .利用裂项求和方法即可得出.
.利用裂项求和方法即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系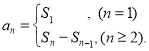 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】在平面上, ![]() ⊥
⊥ ![]() ,|
,| ![]() |=|
|=| ![]() |=1,
|=1, ![]() =
= ![]() +
+ ![]() .若|
.若| ![]() |<
|< ![]() ,则|
,则| ![]() |的取值范围是( )
|的取值范围是( )
A.(0, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣ln(1﹣x),给出以下四个命题: ①x∈(﹣1,1),有f(﹣x)=﹣f(x);
②x1 , x2∈(﹣1,1)且x1≠x2 , 有 ![]() ;
;
③x1 , x2∈(0,1),有 ![]() ;
;
④x∈(﹣1,1),|f(x)|≥2|x|.
其中所有真命题的序号是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正实数a,b,c,函数f(x)=|x+a||x+b|. (Ⅰ)若a=1,b=3,解关于x的不等式f(x)+x+1<0;
(Ⅱ)求证:f(1)f(c)≥16abc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC. 
(Ⅰ)求证:AC⊥BE;
(Ⅱ)若二面角E﹣BA﹣D的余弦值为 ![]() ,求三棱锥A﹣BCD的体积.
,求三棱锥A﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B. 两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C. 由平面三角形的性质,推测空间四边形的性质
D. 在数列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 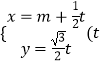 为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为
为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为 ![]() ,且直线l经过椭圆C的右焦点F.
,且直线l经过椭圆C的右焦点F.
(1)求椭圆C的内接矩形PMNQ面积的最大值;
(2)若直线l与椭圆C交于A,B两点,求|FA||FB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com