
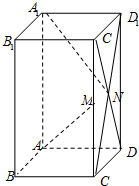
 长方体A1B1C1D1-ABCD中,AB=AD=2,A1A=2$\sqrt{6}$,M为棱C1C的中点,C1D与D1C交于点N,求证:AM⊥A1N.
长方体A1B1C1D1-ABCD中,AB=AD=2,A1A=2$\sqrt{6}$,M为棱C1C的中点,C1D与D1C交于点N,求证:AM⊥A1N. 分析 两条异面直线垂直的证明,通过平行相交,求角是90°即可.或者是建立空间直角坐标系,用向量进行计算.
解答 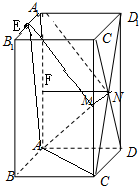 解法一:
解法一:
解:由题意:M为棱C1C的中点,C1D与D1C交于点N,即N是C1D,D1C的中点.
取A1B1的中点E,连接ME,MN.
∵MN${\;}_{=}^{∥}$CD,A1E${\;}_{=}^{∥}$AB,AB=CD.
∴平面MNA1E是平行四边形,则有EM${\;}_{=}^{∥}$A1N;
所以:AM与A1N所成的角是∠AME.
取A1A的中点F,连接NF,由A1B1C1D1-ABCD是长方体:
∴A1FN是直角三角形,A1F=$\frac{1}{2}$A1A=$\sqrt{6}$,FN=$\sqrt{(BC)^{2}+(\frac{1}{2}AB)^{2}}$=$\sqrt{5}$
∴A1N=EM=$\sqrt{11}$
AE=$\sqrt{{(A}_{1}A)^{2}+(\frac{1}{2}AB)^{2}}=5$
AM=$\sqrt{(A{C)}^{2}+(\frac{1}{2}A{A}_{1})}=\sqrt{14}$
在△AME中,∵AE2=AM2+EM2,
∴△AME是直角三角形,∠AME=90°,即AM与A1N所成的角是90°.
故AM⊥A1N,得证.
解法二: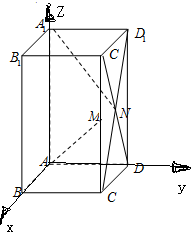
解:以A为原点,以$\left\{{\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{A{A_1}}}\right\}$为正交基底建立空间直角坐标系,
∵AB=AD=2,A1A=2$\sqrt{6}$,M为棱C1C的中点,C1D与D1C交于点N,即中点.
则有A(0,0,0),$M(2,2,\sqrt{6})$,${A_1}(0,0,2\sqrt{6})$,$N(1,2,\sqrt{6})$
∴$\overrightarrow{AM}=(2,2,\sqrt{6})$,$\overrightarrow{{A_1}N}=(1,2,-\sqrt{6})$,
∵$\overrightarrow{AM}•\overrightarrow{{A_1}N}=2×1+2×2+\sqrt{6}×(-\sqrt{6})=0$,
∴AM⊥A1N
点评 本题考查了两条异面直线垂直的证明,常用方法是通过平行相交,求角是90°即可.或者证明其中一条直线垂直另外一条直线所在的平面.或者是建立空间直角坐标系,用向量进行计算.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | B. | $\frac{3}{7}\overrightarrow a-\frac{4}{7}\overrightarrow b$ | C. | $\frac{4}{7}\overrightarrow a+\frac{3}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a-\frac{3}{7}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x<-1或x>2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com