
分析 由题意可知f(x)为定义域内的偶函数,构造函数g(x)=xf(x),由其导函数在x∈(-∞,0)时小于0,可知函数在(-∞,0)上为减函数,又g(x)为奇函数,可知其在(0,+∞)上为减函数,再由函数单调性得答案.
解答 解:∵函数y=f(x)的图象关于y轴对称,∴f(x)为定义域内的偶函数,
当x∈(-∞,0)时,f(x)+x•f'(x)<0,设g(x)=xf(x),
则g′(x)=f(x)+x•f'(x)<0,
∴g(x)在(-∞,0)上为减函数,则在(0,+∞)上为减函数,
∵21>20.2>20=1,0<logπ3<logππ=1,log39=2,
∴0$<lo{g}_{π}3<{2}^{0.2}<lo{g}_{3}9$,
则g(logπ3)>g(20.2)>g(log39).
故答案为:b>a>c.
点评 本题考查利用导数研究函数的单调性,考查了函数构造法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在一次数学竞赛中,30名参赛学生的成绩(百分制)的茎叶图如图所示:若将参赛学生按成绩由高到低编为1-30号,再用系统抽样法从中抽取6人,则其中抽取的成绩在[77,90]内的学生人数为( )
在一次数学竞赛中,30名参赛学生的成绩(百分制)的茎叶图如图所示:若将参赛学生按成绩由高到低编为1-30号,再用系统抽样法从中抽取6人,则其中抽取的成绩在[77,90]内的学生人数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
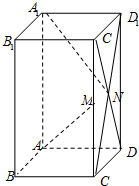 长方体A1B1C1D1-ABCD中,AB=AD=2,A1A=2$\sqrt{6}$,M为棱C1C的中点,C1D与D1C交于点N,求证:AM⊥A1N.
长方体A1B1C1D1-ABCD中,AB=AD=2,A1A=2$\sqrt{6}$,M为棱C1C的中点,C1D与D1C交于点N,求证:AM⊥A1N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | ±$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0) | C. | (1,+∞) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com