
分析 (Ⅰ) 由△ABC的面积公式,利用同角的三角函数关系,即可求出cosB的值;
(Ⅱ)由题意,利用正弦、余弦定理,即可求出AD的值.
解答 解:(Ⅰ) 由题意,△ABC的面积为${S_{△ABC}}=\frac{1}{2}acsinB=accosB$,------------------(1分)
得sinB=2cosB,------①------------(2分)
∵0<B<π,
∴sinB>0,∴cosB>0,--------------------(3分)
又sin2B+cos2B=1,---------②
①代入②得${cos^2}B=\frac{1}{5}$,
∴$cosB=\frac{1}{{\sqrt{5}}}$=$\frac{{\sqrt{5}}}{5}$;-----------(5分)
(Ⅱ)由asinA=5csinC及正弦定理得a2=5c2,---------------(7分)
∵c=2,∴$a=2\sqrt{5}$,
$BD=\frac{1}{2}a=\sqrt{5}$,-----------------(9分)
在△ABD中,由余弦定理得:
$A{D^2}={c^2}+B{D^2}-2BD•c•cosB=4+5-2\sqrt{5}×2×\frac{1}{{\sqrt{5}}}=5$,------(11分)
∴$AD=\sqrt{5}$.--------------------(12分)
点评 本题考查了三角函数求值以及正弦、余弦定理的应用问题,是中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
| 使用时间 | [0,2] | (2,4] | (4,6] |
| 女生人数 | 20 | 20 | z |
| 男生人数 | 20 | 40 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| t | [0,15) | [15,30) | [30,45) | [45,60) | [60,75) | [75,90) |
| 男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
| 女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
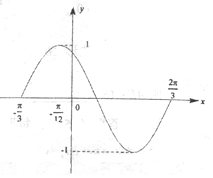 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )| A. | 向左平移$\frac{π}{6}$个单位长度,再把所有点的横坐标扩大到原来的2倍 | |
| B. | 向左平移$\frac{π}{12}$个单位长度.再把所有点的横坐标扩大到原来的2倍 | |
| C. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{12}$个单位长度 | |
| D. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com