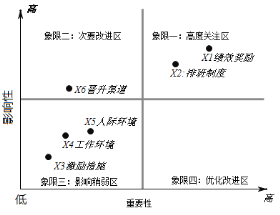
【题目】2020年1月，某公司以问卷的形式调查影响员工积极性的六项关键指标：绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道，在确定各项指标权重结果后，进而得到指标重要性分析象限图（如图）.若客户服务中心从中任意抽取不同的两项进行分析，则这两项来自影响稍弱区的概率为（ ）
A.
B.
C.
D.
世纪百通期末金卷系列答案科目：高中数学 来源： 题型：
【题目】数列
：
，
，
，…，
，…，对于给定的
（
，
），记满足不等式：
（
，
）的
构成的集合为
．
（Ⅰ）若数列
，写出集合
；
（Ⅱ）如果（，）均为相同的单元素集合，求证：数列，，…，，…为等差数列；
（Ⅲ）如果（，）为单元素集合，那么数列，，…，，…还是等差数列吗？如果是等差数列，请给出证明；如果不是等差数列，请给出反例．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】新中国昂首阔步地走进2019年，迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动，规则如下：共有30道单选题，每题4个选项中只有一个正确，每答对一题获得5颗红星，每答错一题反扣2颗红星；若放弃此题，则红星数无变化.答题所获得的红星可用来兑换神秘礼品，红星数越多奖品等级越高.小强参加该活动，其中有些题目会做，有些题目可以排除若干错误选项，其余的题目则完全不会.
（1）请问：对于完全不会的题目，小强应该随机从4个选项中选一个作答，还是选择放弃？（利用统计知识说明理由）
（2）若小强有12道题目会做，剩下的题目中，可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是
.请问：小强在本次活动中可以获得最多红星数的期望是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，四边形
为平行四边形，
，
平面，
，
，
，且
是
的中点.
（Ⅰ）求证：
平面
；
（Ⅱ）求二面角
的大小；
（Ⅲ）在线段
上是否存在一点
，使得
与
所成的角为
？ 若存在，求出
的长度；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，点
，直线
与动直线
的交点为
，线段
的中垂线与动直线
的交点为
．
（1）求动点
的轨迹
的方程；
（2）过动点
作曲线
的两条切线，切点分别为
， 
，求证： 
的大小为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
与过其右焦点F（1，0）的直线交于不同的两点A，B，线段AB的中点为D，且直线l与直线OD的斜率之积为
.
（1）求C的方程；
（2）设椭圆的左顶点为M，kMA，kMB分别表示直线MA，MB的斜率，求证
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学，分形的外表结构极为复杂，但其内部却是有规律可寻的．一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统．下面我们用分形的方法来得到一系列图形，如图1，线段
的长度为a，在线段上取两个点C、D，使得
，以
为一边在线段的上方做一个正六边形，然后去掉线段，得到图2中的图形；对图二中的最上方的线段
作相同的操作，得到图3中的图形；依次类推，我们就得到了以下一系列图形；
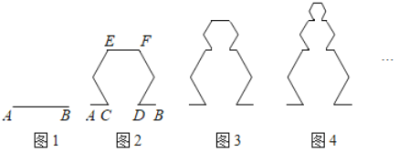
记第n个图形（图1为第1个图形）中的所有线段长的和为
，若对任意的正整数n，都有
．则正数a的最大值为______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD中，
，
，E，F分别为AD，AB中点，M为线段BC上的一个动点，现将
，
，分别沿EC，EF折起，使A，D重合于点P．设PM与平面BCEF所成角为
，二面角
的平面角为
，二面角
的平面角为
，则（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
