
已知a为实数, 。
。
⑴求导数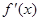 ;
;
⑵若 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
⑶若 在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
⑴
⑵f(x)在[-2,2]上的最大值为 最小值为
最小值为
⑶a的取值范围是[-2,2].
解析试题分析:⑴由原式得 ∴
∴
⑵由 得
得 ,此时有
,此时有 .
.
由 得
得 或x="-1" , 又
或x="-1" , 又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为
⑶解法一: 的图象为开口向上且过点(0,-4)的抛物线,由条件得
的图象为开口向上且过点(0,-4)的抛物线,由条件得
即 ∴-2≤a≤2.
∴-2≤a≤2.
所以a的取值范围为[-2,2].
解法二:令 即
即 由求根公式得:
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时, 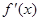 ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得-2≤a≤2.
解不等式组得-2≤a≤2.
∴a的取值范围是[-2,2].
考点:导数计算,利用导数研究函数的单调性、极值、最值。
点评:中档题,此类问题较为典型,是导数应用的基本问题。在某区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。求最值应遵循“求导数,求驻点,计算极值及端点函数值,比较确定最值”。


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:解答题
已知函数
(1)当 时,求
时,求 在
在 上的最小值;
上的最小值;
(2)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函 数 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;
(2)若对于 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围;
(3)记 .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
市内电话费是这样规定的,每打一次电话不超过3分钟付电话费0.18元,超过3分钟而不超过6分钟的付电话费0.36元,依次类推,每次打电话
 分钟应付话费y元,写出函数解析式并画出函数图象.
分钟应付话费y元,写出函数解析式并画出函数图象.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax3+bx2-x(x∈R,a、b是常数,a≠0),且当x=1和x=2时,函数f(x)取得极值.(I)求函数f(x)的解析式;
(Ⅱ)若曲线y=f(x)与g(x)=
 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com