
分析 (Ⅰ)法一:通过讨论2x-4的范围,得到关于x的不等式组,解出取并集;法二:根据题意得出x≥0,再去绝对值即可,法三:根据题意得出x≥0,两边平方解出即可;
(Ⅱ)法一:问题转化为f(x+1)>f(1)对?x∈(0,+∞)恒成立,结合函数的单调性问题,求出a的范围即可;法二:等价于(2x+2-a)2>(2-a)2对?x∈(0,+∞)恒成立,求出a的范围即可.
解答 解:(Ⅰ)若a=4,则f(x)≤x可化为|2x-4|≤x,
法1:即$\left\{\begin{array}{l}2x-4≤0\\ 4-2x≤x\end{array}\right.$或$\left\{\begin{array}{l}2x-4≥0\\ 2x-4≤x\end{array}\right.$,
解得$\frac{4}{3}≤x≤4$,
所以f(x)≤x的解集为$\left\{{x|\frac{4}{3}≤x≤4}\right\}$;
法2:即$\left\{\begin{array}{l}x≥0\\ 2x-4≤x\\ 2x-4≥-x\end{array}\right.$,
解得$\frac{4}{3}≤x≤4$,
所以f(x)≤x的解集为$\left\{{x|\frac{4}{3}≤x≤4}\right\}$;
法3:即$\left\{\begin{array}{l}x≥0\\{({2x-4})^2}≤{x^2}\end{array}\right.$,
即$\left\{\begin{array}{l}x≥0\\ 3{x^2}-16x+16≤0\end{array}\right.$解得$\frac{4}{3}≤x≤4$,
所以f(x)≤x的解集为$\left\{{x|\frac{4}{3}≤x≤4}\right\}$;
(Ⅱ)法1:f(x+1)>|2-a|对?x∈(0,+∞)恒成立
即f(x+1)>f(1)对?x∈(0,+∞)恒成立,
又因为f(x)=|2x-a|在$({-∞,\frac{a}{2}}]$上单调递减,在$[{\frac{a}{2},+∞})$上单调递增,
所以$\frac{a}{2}≤1$解得a≤2,
所以实数a的取值范围为(-∞,2];
法2:f(x+1)>|2-a|对?x∈(0,+∞)恒成立
即|2x+2-a|>|2-a|对?x∈(0,+∞)恒成立
等价于(2x+2-a)2>(2-a)2对?x∈(0,+∞)恒成立,
即a<2+x对?x∈(0,+∞)恒成立,
所以a≤2…(9分)
所以实数a的取值范围为(-∞,2].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
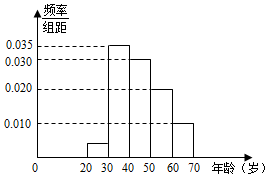 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
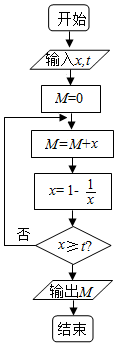
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2 | C. | 2n | D. | $\frac{n}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com