
 (a,b为常数).
(a,b为常数). 与
与 的大小.
的大小. 在R上是增函数,再利用基本不等式得出
在R上是增函数,再利用基本不等式得出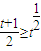 ,下面就m的取值分类讨论,即可得出结果.
,下面就m的取值分类讨论,即可得出结果.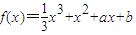 在R上是增函数,
在R上是增函数,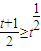 ,
,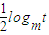 ≤
≤ ,∴
,∴ ≤
≤ ;
;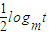 ≥
≥ ,
,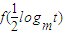 ≥
≥ .
.

科目:高中数学 来源:全优设计必修五数学苏教版 苏教版 题型:013
已知Sk为数列{an}的前k项和,且Sk+Sk+1=ak+1(k∈N+).那么此数列是
A.单调增数列
B.单调减函数
C.常数列
D.摆动数列
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:022
(1)已知x![]() ,函数y=4x-2+
,函数y=4x-2+![]() 的最大值为________.
的最大值为________.
(2)已知x>0,y>0,且![]() ,x+y的最小值为________.
,x+y的最小值为________.
(3)已知a、b为常实数,函数y=(x-a)2+(x-b)2的最小值为________.
查看答案和解析>>
科目:高中数学 来源:同步题 题型:单选题
 ,则
,则 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com