
【题目】2017年10月,举世瞩目的中国共产党第十九次全国代表大会在北京顺利召开.某高中为此组织全校2000名学生进行了一次“十九大知识知多少”的问卷测试(满分:100分),并从中抽取了40名学生的测试成绩,得到了如图所示的频率分布直方图.

(1)求图中实数![]() 的值及样本中40名学生测试成绩的平均数和中位数(同一组中的数据用该组区间的中点值作代表);
的值及样本中40名学生测试成绩的平均数和中位数(同一组中的数据用该组区间的中点值作代表);
(2)(i)利用分层抽样的方法从成绩低于70分的三组学生中抽取7人,再从这7人中随机抽取2人分析成绩不理想的原因,求前2组中至少有1人被抽到的概率;
(2)以频率估计概率,试估计该校这次测试成绩不低于80分的学生人数.
【答案】(1)![]() ,平均数74,中位数75(2)
,平均数74,中位数75(2)![]() ,700
,700
【解析】试题分析:(1)根据图中所有小矩形的面积之和等于1,解得![]() ;根据组中值与对应区间概率乘积的和计算平均数,根据中位数定义计算中位数,(2)先根据分层抽样得前3组学生分别抽取1人,2人,4人,再利用枚举法确定基本事件总数,从中确定前2组中至少有1人被抽到的事件数,最后根据古典概型概率公式求概率;先求不低于80分的频率,再乘以总数得频数,即为测试成绩不低于80分的学生人数.
;根据组中值与对应区间概率乘积的和计算平均数,根据中位数定义计算中位数,(2)先根据分层抽样得前3组学生分别抽取1人,2人,4人,再利用枚举法确定基本事件总数,从中确定前2组中至少有1人被抽到的事件数,最后根据古典概型概率公式求概率;先求不低于80分的频率,再乘以总数得频数,即为测试成绩不低于80分的学生人数.
试题解析:解:(1)由于图中所有小矩形的面积之和等于1,
所以![]() ,解得
,解得![]() ,
,
故样本中40名学生的测试成绩的平均数![]() ,
,
设这40名学生的测试成绩的中位数为![]() ,由于前3组频率之和为0.35,前4组频率之和为0.65,故中位数落在第4组,于是有
,由于前3组频率之和为0.35,前4组频率之和为0.65,故中位数落在第4组,于是有![]() ,解得
,解得![]() .
.
即这40名学生的测试成绩的中位数为75.
(2)(i)由分层抽样知识可知,前3组学生分别抽取1人,2人,4人,记第1小组的1名学生为![]() ,第2小组的2名学生分别为
,第2小组的2名学生分别为![]() ,
, ![]() ,第3组的4名学生分别为
,第3组的4名学生分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,从中任取2人的所有可能结果为:
,从中任取2人的所有可能结果为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共21种,
,共21种,
其中前2组中至少有1人被抽到的可能结果为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共15种,
,共15种,
故所求的概率![]() .
.
(ii)样本中测试成绩不低于80分的频率为![]() ,将0.35视为频率值,
,将0.35视为频率值,
则该校这次测试成绩不低于80分的学生人数约为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图②所示.
AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图②所示.

(1)证明:平面ABD⊥平面BCD;
(2)求二面角DABC的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300千米的海面
方向300千米的海面![]() 处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.若![]() 是函数
是函数![]() 的零点,则
的零点,则![]() 是
是![]() 的整数倍
的整数倍
B.函数![]() 的图象关于点
的图象关于点![]() 对称
对称
C.函数![]() 的图象与函数
的图象与函数![]() 的图象相同
的图象相同
D.函数![]() 的图象可由
的图象可由![]() 的图象先向上平移
的图象先向上平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 的两个交点分别为
的两个交点分别为![]() ,
, ![]() ,求证:
,求证: 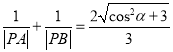 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校学生喜欢吃零食是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人,抽到不喜欢吃零食的学生的概率为![]() .
.
喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(Ⅰ)请将上面的列表补充完整;
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.
下面的临界值表供参考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某火锅店为了了解气温对营业额的影响,随机记录了该店1月份其中5天的日营业额y(单位:万元)与该地当日最低气温x(单位:℃)的数据,如下表:
![]()
(1)求y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2)判断y与x之间是正相关还是负相关,若该地1月份某天的最低气温为6 ℃,用所求回归方程预测该店当日的营业额;
(3)设该地1月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2,求P(3.8<X≤13.4).
,σ2近似为样本方差s2,求P(3.8<X≤13.4).
附:①回归方程![]() 中,
中,![]() =
=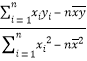 ,
,![]() =
=![]() ﹣
﹣![]() .
.
②![]() ≈3.2,
≈3.2,![]() ≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com