
【题目】若正项数列{![]() }满足:
}满足:![]() ,则称此数列为“比差等数列”.
,则称此数列为“比差等数列”.
(1)请写出一个“比差等数列”的前3项的值;
(2)设数列{![]() }是一个“比差等数列”
}是一个“比差等数列”
(i)求证:![]() ;
;
(ii)记数列{![]() }的前
}的前![]() 项和为
项和为![]() ,求证:对于任意
,求证:对于任意![]() ,都有
,都有![]() .
.
【答案】(1)2,4,![]() ;(2)(i)见解析(ii)见解析
;(2)(i)见解析(ii)见解析
【解析】试题分析:(1)由题意可得![]() ,由迭代法,例如代入
,由迭代法,例如代入![]() ,可依次得到
,可依次得到![]() 。(2)由
。(2)由![]() ,可知
,可知![]() 又
又![]() ,所以
,所以![]() 即
即![]() ,由均值不等式
,由均值不等式![]() 。由
。由![]() >0,可知数列{
>0,可知数列{![]() }单调递增。所以
}单调递增。所以![]() >1,
>1,
由a2≥4得,a3﹣a2≥1,a4﹣a3≥1,…,an﹣an﹣1≥1,
以上 n﹣1个不等式相加得,an≥(n﹣2)+4=n+2(n≥2),所以
当n≥2时,Sn=a1+a2+a3+…+an
≥1+4+(3+2)+…+(n+2)≥(1+2)+(2+2)+…+(n+2)﹣2
=![]() ﹣2=
﹣2=![]() 检验n=1也符合,即证。
检验n=1也符合,即证。
试题解析:(1)解:一个“比差等数列”的前3项可以是:2,4,![]() ;
;
(2)(i)证明:当n=1时,![]() ,
,
∴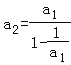 =
=![]() =
=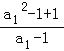 =
=![]() ,
,
∵an>0,∴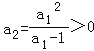 ,则a1﹣1>0,即a1>1,
,则a1﹣1>0,即a1>1,
∴![]() ≥2
≥2![]() +2=4,
+2=4,
当且仅当![]() 时取等号,
时取等号,
则a2≥4成立;
(ii)由an>0得,an+1﹣an=![]() ≥0,
≥0,
∴an+1≥an>0,则an+1﹣an=![]() ,
,
由a2≥4得,a3﹣a2≥1,a4﹣a3≥1,…,an﹣an﹣1≥1,
以上 n﹣1个不等式相加得,an≥(n﹣2)+4=n+2(n≥2),
当n≥2时,Sn=a1+a2+a3+…+an
≥1+4+(3+2)+…+(n+2)≥(1+2)+(2+2)+…+(n+2)﹣2
=![]() ﹣2=
﹣2=![]() ,
,
当n=1时,由(i)知S1=a1>1≥![]() ,
,
综上可得,对于任意n∈N*,都有Sn>![]() .
.


科目:高中数学 来源: 题型:
【题目】下列是关于函数y=f(x),x∈[a,b]的几个命题:
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为 ( )
A. 0 B. 1 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】否定“自然数![]() 、
、![]() 、
、![]() 中恰有一个偶数”时正确的反设为( )
中恰有一个偶数”时正确的反设为( )
A. ![]() 、
、![]() 、
、![]() 都是奇数 B.
都是奇数 B. ![]() 、
、![]() 、
、![]() 至少有两个偶数
至少有两个偶数
C. ![]() 、
、![]() 、
、![]() 都是偶数 D.
都是偶数 D. ![]() 、
、![]() 、
、![]() 中都是奇数或至少有两个偶数
中都是奇数或至少有两个偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沭阳县某水果店销售某种水果,经市场调查,该水果每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() 近似满足关系式
近似满足关系式![]() ,其中
,其中![]() 为常数,已知销售价格定为
为常数,已知销售价格定为![]() 元
元![]() 千克时,每日可销售出该水果
千克时,每日可销售出该水果![]() 千克.
千克.
(1)求实数![]() 的值;
的值;
(2)若该水果的成本价格为![]() 元
元![]() 千克,要使得该水果店每日销售该水果获得最大利润,请你确定销售价格
千克,要使得该水果店每日销售该水果获得最大利润,请你确定销售价格![]() 的值,并求出最大利润.
的值,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有将;某顾客从此10张券中任取2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值![]() (元)的概率分布列.
(元)的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)可近似看作一次函数
(元/件)可近似看作一次函数![]() 的关系(如图所示).
的关系(如图所示).
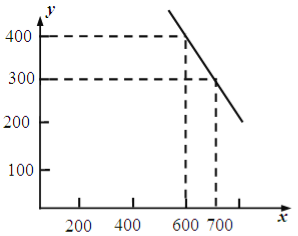
(1)根据图象,求一次函数![]() 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价—成本总价)为![]() 元. 试用销售单价
元. 试用销售单价![]() 表示毛利润
表示毛利润![]() 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com