
【题目】已知向量![]() 为正实数,
为正实数, ![]() .
.
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)是否存在![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)不存在
;(2)不存在![]() ,使
,使![]() .
.
【解析】试题分析:(1)若![]() ⊥
⊥![]() ,则
,则![]() ·
·![]() =0,即(-2t2-1)(-
=0,即(-2t2-1)(-![]() -
-![]() )+(t2+3)(-
)+(t2+3)(-![]() +
+![]() )=0,得k=
)=0,得k=![]() =
=![]() ≤
≤![]() ,从而得解;
,从而得解;
(2)假设存在正实数k,t,使![]() ∥
∥![]() ,则(-2t2-1)(-
,则(-2t2-1)(-![]() +
+![]() )-(t2+3)(-
)-(t2+3)(-![]() -
-![]() )=0,整理得t3+t+k=0,从而得解.
)=0,整理得t3+t+k=0,从而得解.
试题解析:
![]() =(1,2)+(t2+1)(-2,1)=(-2t2-1,t2+3),
=(1,2)+(t2+1)(-2,1)=(-2t2-1,t2+3), ![]() =(-
=(-![]() -
-![]() ,-
,- ![]() +
+![]() ).
).
(1)若![]() ⊥
⊥![]() ,则
,则![]() ·
·![]() =0,即(-2t2-1)(-
=0,即(-2t2-1)(-![]() -
-![]() )+(t2+3)(-
)+(t2+3)(-![]() +
+![]() )=0,
)=0,
整理得,k=![]() =
=![]() ≤
≤![]() ,当且仅当
,当且仅当![]() ,即t=1时取等号,∴kmax=
,即t=1时取等号,∴kmax=![]() .
.
(2)假设存在正实数k,t,使![]() ∥
∥![]() ,则(-2t2-1)(-
,则(-2t2-1)(-![]() +
+![]() )-(t2+3)(-
)-(t2+3)(-![]() -
-![]() )=0,化简得
)=0,化简得![]() =0,即t3+t+k=0.
=0,即t3+t+k=0.
因为k,t是正实数,故满足上式的k,t不存在,所以不存在k,t,使![]() ∥
∥![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取![]() 名进行调查,将受访用户按年龄分成
名进行调查,将受访用户按年龄分成![]() 组:
组: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于![]() 岁的概率;
岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
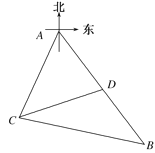
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.
的值;若不存在,请说理由.
(参考数据: ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.

(Ⅰ)证明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解本校学生网课期间课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
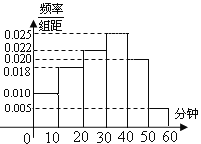
(1)根据频率分布直方图估计抽取样本的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)已知样本中玩电脑游戏时长在![]() 的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值);
(Ⅲ)使用若干年后,对机床的处理方案有两种:
(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(2)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com