
【题目】据权威部门统计,高中学生眼睛近视已是普遍现象,这与每个学生是否科学用眼有很大关系.每年5月5日是全国爱眼日,我市某中学在此期间开展了一系列的用眼卫生教育活动.为了解本校学生用眼卫生情况,学校医务室随机抽取了100名学生对其进行调查,下面是根据调查结果绘制的学生不间断用眼时间(单位:分钟)的频率分布直方图,且将不间断用眼时间不低于60分钟的学生称为“不爱护眼者”,低于60分钟的学生称为“爱护眼者”.
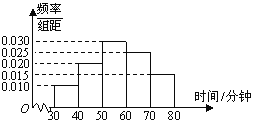
(1)根据频率分布直方图,求这100名学生不间断用眼时间的平均数和中位数(结果精确到0.1);
(2)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“不爱护眼者”与性别有关?
爱护眼者 | 不爱护眼者 | 合计 | |
男 | 45 | ||
女 | 15 | ||
合计 |
(3)在不间断用眼时间为![]() 和
和![]() 两组人中先按分层抽样的方法任意选取5人,再从这5人中随机抽取2人了解他们的视力状况,求这两人来自不同组别的概率.
两组人中先按分层抽样的方法任意选取5人,再从这5人中随机抽取2人了解他们的视力状况,求这两人来自不同组别的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1)平均数为![]() ,中位数为
,中位数为![]() .(2)
.(2)![]() 列联表答案见解析,有99%的把握认为“不爱护眼者”与性别有关.(3)
列联表答案见解析,有99%的把握认为“不爱护眼者”与性别有关.(3)![]()
【解析】
(1)分别利用平均数和中位数的公式求解.
(2)根据频率分布直方图可得到爱护眼者人数,不爱护眼者的人数,由此完成![]() 列联表,然后根据列联表,由公式
列联表,然后根据列联表,由公式![]() 求得
求得![]() ,再与临界表对比下结论.
,再与临界表对比下结论.
(3)根据频率分布直方图知,在这两组中分别取2人和3人,用字母分别表示为![]() .列举出基本事件总数,找出这两人来自不同组别的基本事件数,代入古典概型的概率公式求解.
.列举出基本事件总数,找出这两人来自不同组别的基本事件数,代入古典概型的概率公式求解.
(1)这100个同学不间断用眼时间的平均数为
![]()
设其中位数为![]() ,则
,则![]()
解得![]()
(2)由频率分布直方图知,爱护眼者人数为![]() 人,
人,
不爱护眼者为![]() 人,由此得
人,由此得![]() 列联表
列联表
爱护眼者 | 不爱护眼者 | 合计 | |
男 | 20 | 25 | 45 |
女 | 40 | 15 | 55 |
合计 | 60 | 40 | 100 |
![]()
所以,有99%的把握认为“不爱护眼者”与性别有关.
(3)由频率分布直方图知,在这两组中分别取2人和3人,用字母分别表示为![]() .设事件C:“这两人来自不同组别”,
.设事件C:“这两人来自不同组别”,
其基本事件有:![]()
![]() 共10个,
共10个,
事件C包含基本事件有:![]() ,
,
![]() 共6个,
共6个,
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,与此同时,相关管理部门推出了针对电商商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品好评率为![]() ,对服务好评率为
,对服务好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若针对商品的好评率,采用分层抽样的方式这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
注:1.
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注:2.![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点 A(a , b),抛物线C :![]() (a ≠0 , b ≠0 , a ≠2p).过点 A 作直线l ,交抛物线 C 于点P 、Q .如果以线段 PQ 为直径的圆过抛物线C 的顶点,求直线 l 的方程
(a ≠0 , b ≠0 , a ≠2p).过点 A 作直线l ,交抛物线 C 于点P 、Q .如果以线段 PQ 为直径的圆过抛物线C 的顶点,求直线 l 的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
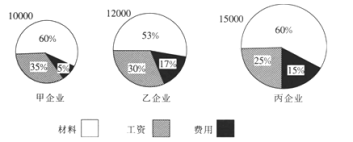
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,我国继续实行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有![]() 人,现采用分层抽样的方法,从该单位上述员工中抽取50人调查专项附加扣除的享受情况.
人,现采用分层抽样的方法,从该单位上述员工中抽取50人调查专项附加扣除的享受情况.
(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的50人中,享受至少两项专项附加扣除的员工有5人,分别记为![]() .享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这5人中随机抽取2人接受采访.
.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这5人中随机抽取2人接受采访.
员工 项目 | A | B | C | D | E |
子女教育 | ○ | ○ | × | ○ | × |
继续教育 | × | × | ○ | × | ○ |
大病医疗 | × | ○ | × | ○ | × |
住房贷款利息 | ○ | ○ | × | × | ○ |
住房租金 | × | × | ○ | ○ | × |
赡养老人 | ○ | ○ | × | × | × |
(1)试用所给字母列举出所有可能的抽取结果;
(2)设![]() 为事件“抽取的2人享受的专项附加扣除全都不相同”,求事件
为事件“抽取的2人享受的专项附加扣除全都不相同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com