
����Ŀ��֧��������֧����Ŀǰ�г�ռ���ʽϸߵ�֧����ʽ��ij���������л�����ʹ��������֧����ʽ���������˶Ա�.��ȫ�������ȡ��100��������Ϊ�о������������˸�������������ʹ����������Ƶ�ʷֲ�ֱ��ͼ��ͼ.
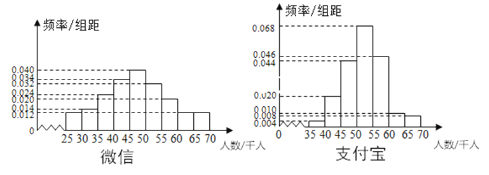
��1����A��ʾ�¼�����֧����������50ǧ����������A�ĸ��ʣ�
��2����д�������������������������ж��Ƿ���99%�İ�����Ϊ֧��������֧����ʽ�йأ�

��3������֧��������Ƶ�ʷֲ�ֱ��ͼ��������֧����ʽ�����ӽ��бȽ�.
����

K2![]()
���𰸡���1��0.62����2����![]() �İ�����Ϊ֧��������֧����ʽ�йأ���3��֧����֧������������֧��
�İ�����Ϊ֧��������֧����ʽ�йأ���3��֧����֧������������֧��
��������
![]() �ɵ�һ��Ƶ�ʷֲ�ֱ��ͼ��ֱ�Ӽ��㡰��֧����������50ǧ�ˡ���Ƶ��,��Ϊ�¼�A�ĸ���;
�ɵ�һ��Ƶ�ʷֲ�ֱ��ͼ��ֱ�Ӽ��㡰��֧����������50ǧ�ˡ���Ƶ��,��Ϊ�¼�A�ĸ���;
![]() ����Ƶ�ʷֲ�ֱ��ͼ��ȫ
����Ƶ�ʷֲ�ֱ��ͼ��ȫ![]() ������,�����������е����ݴ��빫ʽ����۲�ֵ
������,�����������е����ݴ��빫ʽ����۲�ֵ![]() ,�������ٽ�ֵ�����ɵó�����;
,�������ٽ�ֵ�����ɵó�����;
![]() ����Ƶ�ʷֲ�ֱ��ͼ�ֱ�������֧����֧����֧��100������֧��������ƽ��ֵ,�Ƚ�����ƽ��ֵ�Ĵ�С����.
����Ƶ�ʷֲ�ֱ��ͼ�ֱ�������֧����֧����֧��100������֧��������ƽ��ֵ,�Ƚ�����ƽ��ֵ�Ĵ�С����.
![]() ��������,����֧��������Ƶ�ʷֲ�ֱ��ͼ�ɵ�,
��������,����֧��������Ƶ�ʷֲ�ֱ��ͼ�ɵ�,![]() ,
,
������֧����������50ǧ�˵ĸ���Ϊ![]() ��
��
![]() ����Ƶ�ʷֲ�ֱ��ͼ�е�����,��ȫ
����Ƶ�ʷֲ�ֱ��ͼ�е�����,��ȫ![]() ����������:
����������: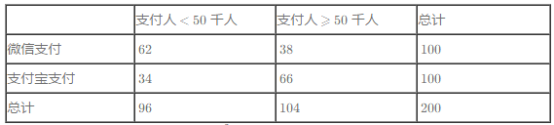
����![]() ,
,
������![]() �İ�����Ϊ֧��������֧����ʽ�йأ�
�İ�����Ϊ֧��������֧����ʽ�йأ�
![]() ��Ƶ�ʷֲ�ֱ��ͼ�ɵ�,��֧��100������֧��������ƽ��ֵΪ:
��Ƶ�ʷֲ�ֱ��ͼ�ɵ�,��֧��100������֧��������ƽ��ֵΪ:
![]()
![]() ��
��
֧����֧��100������֧��������ƽ��ֵΪ:
![]()
![]() ��
��
��Ϊ![]() ,����֧����֧������������֧��.
,����֧����֧������������֧��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ������������⣺��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ�����˼�ǣ�һ��7����������381յ�ƣ������������е���һ���������һ�������2���������Ķ��㹲�еƣ� ��
A. 1յ B. 3յ C. 5յ D. 9յ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����һ�����Ϸ���������£��Ƚ�һ���ӷ�����ͼ��ʾ������![]() ���߳�Ϊ2����λ���Ķ���
���߳�Ϊ2����λ���Ķ���![]() ����Ȼ��ͨ����������ȷ�������������εı߰���ʱ�뷽�����ߵĵ�λ����������ĵ���Ϊ
����Ȼ��ͨ����������ȷ�������������εı߰���ʱ�뷽�����ߵĵ�λ����������ĵ���Ϊ![]() �������ӾͰ���ʱ�뷽������
�������ӾͰ���ʱ�뷽������![]() ����λ��һֱѭ����ȥ.��ij�������������Ӻ�����ǡ���ֻص���
����λ��һֱѭ����ȥ.��ij�������������Ӻ�����ǡ���ֻص���![]() �������в�ͬ�߷����У� ��
�������в�ͬ�߷����У� ��

A. 22�� B. 24�� C. 25�� D. 27��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�
�ȱߡ�ABC�ı߳�Ϊ3����D��E�ֱ�ΪAB��AC�ϵĵ㣬������![]() ����ͼ�٣�������ADE��DE����A1DE��λ�ã�ʹ�����A1��DE��B��ֱ����ǣ�����A1B��A1C����ͼ�ڣ�.
����ͼ�٣�������ADE��DE����A1DE��λ�ã�ʹ�����A1��DE��B��ֱ����ǣ�����A1B��A1C����ͼ�ڣ�.
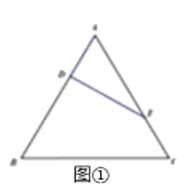
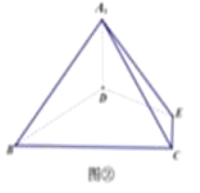
��1����֤��A1D��ƽ��BCED��
��2�����߶�BC���Ƿ���ڵ�P���������˵㣩��ʹֱ��PA1��ƽ��A1BD���ɵĽ�Ϊ60���������ڣ����A1P�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʹ�����Ժ��һ�ڼ�ͬʱ�ٰ조Ϸ���Ļ�չ�������������Ѵ���չ��������������ɽˮ��չ���� �������\�黭չ���ĸ�չ����ijͬѧ��������һ������ϡ�������ι����е�һ���������ٲι�һ����չ����ͬ�IJι۷�������
A. 6�� B. 8�� C. 10�� D. 12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
Ϊ������![]() Ϊֱ��
Ϊֱ��![]() ����б�ǣ���������ԭ��
����б�ǣ���������ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ��������Ϊ���ᣬ����������ϵ������
��������Ϊ���ᣬ����������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��д������![]() ��ֱ�����귽�̣�����
��ֱ�����귽�̣�����![]() ʱֱ��
ʱֱ��![]() ����ͨ���̣�
����ͨ���̣�
��2��ֱ��![]() ������
������![]() ��������
��������![]() ����
����![]() ��ֱ������Ϊ
��ֱ������Ϊ![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
������![]() ������
������![]() ��
��![]() �ĵ������䣻
�ĵ������䣻
������![]() ��3����ͬ��ʵ������ʵ��
��3����ͬ��ʵ������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����![]() ʱ�������������
ʱ�������������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������������������
��������������������![]() ��ȡֵ�ļ���.
��ȡֵ�ļ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����xex��g��x����a��lnx+x��.
��1����a��eʱ����֤��f��x����g��x���������
��2����a��0ʱ����֤��f��x����g��x��+1���н�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4��5������ʽѡ��]
��֪����![]() ��
��
��1����![]() ʱ����ʽ
ʱ����ʽ![]() �Ľ⼯��
�Ľ⼯��
��2��������ʽ![]() �Ľ⼯����
�Ľ⼯����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com