
分析 (1)根据数列的递推公式可得{an+1-an}是首项为2,公比为2的等比数列,再利用迭代法即可求出数列{an}的通项公式;
(2)可得数列{bn}的通项,{cn}的通项公式,再分组求和即可.
解答 解:(1)由 an+2=3an+1-2an,得an+2-an+1=2(an+1-an),
又a1=1,a2=3,所以a2-a1=2
所以{an+1-an}是首项为2,公比为2的等比数列.
所以${a_{n+1}}-{a_n}={2^n}$,
所以${a_n}={a_1}+({{a_2}-{a_1}})+…+({{a_n}-{a_{n-1}}})=1+{2^1}+{2^2}+…+{2^{n-1}}={2^n}-1$.
(2)∵${a_n}={2^n}-1$,
∴${b_n}=4{log_2}({{2^n}-1+1})+3$=4n+3,
${c_n}=\frac{2^n}{{({{2^n}-1})?¤({{2^{n+1}}-1})}}=\frac{{({{2^{n+1}}-1})-({{2^n}-1})}}{{({{2^n}-1})?¤({{2^{n+1}}-1})}}=\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}}$,
记数列{(-1)nbnbn+1}的前n项和为Sn,
则S2n=(-b1b2+b2b3)+(-b3b4+b4b5)+…+(-b2n-1b2n+b2nb2n+1)
=$2d({b_2}+{b_4}+…+{b_{2n}})=8×\frac{{n({{b_2}+{b_{2n}}})}}{2}=4n({11+8n+3})=32{n^2}+56n$.
记数列{cn}的前n项和为Tn,
则T2n=c1+c2+…+c2n═$({\frac{1}{{{2^1}-1}}-\frac{1}{{{2^2}-1}}})+({\frac{1}{{{2^2}-1}}-\frac{1}{{{2^3}-1}}})+…+({\frac{1}{{{2^{2n-1}}-1}}-\frac{1}{{{2^{2n}}-1}}})+({\frac{1}{{{2^{2n}}-1}}-\frac{1}{{{2^{2n+1}}-1}}})$=$\frac{1}{{{2^1}-1}}-\frac{1}{{{2^{2n+1}}-1}}$=$1-\frac{1}{{{2^{2n+1}}-1}}$.
所以数列{(-1)nbnbn+1+cn}的前n项和为$32{n^2}+56n+1-\frac{1}{{{2^{2n+1}}-1}}$.
点评 该题考查等差数列等比数列的通项公式、求和公式,裂项求和,属于中档题.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
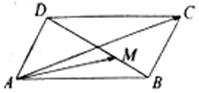 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,e2-e+1] | B. | [0,e2+e-1] | C. | [0,e2+e+1] | D. | [0,e2-e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com