
已知集合 ={
={ |在定义域内存在实数
|在定义域内存在实数 ,使得
,使得 成立}
成立}
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)证明:函数 ;.
;.
(Ⅲ)设函数 ,求实数a的取值范围.
,求实数a的取值范围.
科目:高中数学 来源:2015届山东省高二下学期期中检测理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)若 在
在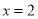 时有极值,求实数
时有极值,求实数 的值和
的值和 的极大值;
的极大值;
(2)若 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中质量检测试卷(解析版) 题型:解答题
已知函数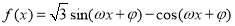 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(1)求 的值;
的值;
(2)将函数 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中质量检测试卷(解析版) 题型:选择题
以下结论:①若 ,则
,则 ;②若
;②若 ,则存在实数
,则存在实数 ,使
,使 ;
;
③若 是非零向量,
是非零向量, ,那么
,那么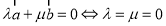 ;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )
;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )
A、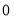 B、
B、 C、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期末理科数学试卷(解析版) 题型:解答题
设函数 ,其中
,其中 ;
;
(Ⅰ)若 的最小正周期为
的最小正周期为 ,求
,求 的单调增区间;
的单调增区间;
(Ⅱ)若函数 的图象的一条对称轴为
的图象的一条对称轴为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数 表示过原点的曲线,且在
表示过原点的曲线,且在 处的切线的倾斜角均为
处的切线的倾斜角均为 ,有以下命题:
,有以下命题:
① 的解析式为
的解析式为 ;
;
② 的极值点有且只有一个;
的极值点有且只有一个;
③ 的最大值与最小值之和等于零;
的最大值与最小值之和等于零;
其中正确命题的序号为_ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com