Question

19．已知三棱锥P-ABC中，PA，PB，PC两两垂直，PA=PB=2，其外接球的表面积为24π，则外接球球心到平面ABC的距离为$\frac{2}{3}$．

Answer 1

分析 设球的半径为R，由已知可求R²=6，将P-ABC视为正四棱柱的一部分，可求CD，PC，利用余弦定理可求cos∠ACB，利用同角三角函数基本关系式可求sin∠ACB，进而可求△ABC外接圆的半径为r，设球心到平面ABC的距离为d，由d=$\sqrt{{R}^{2}-{r}^{2}}$即可得解．

解答 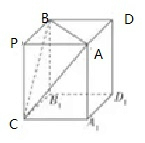解：设球的半径为R，则由4πR²=24π，可得：R²=6，
如图所示，将P-ABC视为正四棱柱的一部分，
则CD=2R，即PA²+PB²+PC²=4R²=24，可得PC=4，
因为AB=2$\sqrt{2}$，AC=BC=2$\sqrt{5}$，
所以cos∠ACB=$\frac{20+20-8}{2×2\sqrt{5}×2\sqrt{5}}$=$\frac{4}{5}$，sin∠ACB=$\frac{3}{5}$，△ABC外接圆的半径为r=$\frac{5\sqrt{2}}{3}$，
设球心到平面ABC的距离为d，
所以d=$\sqrt{{R}^{2}-{r}^{2}}$=$\sqrt{6-\frac{50}{9}}$=$\frac{2}{3}$．
故答案为：$\frac{2}{3}$．

点评 本题主要考查了余弦定理，同角三角函数基本关系式，球内接多面体的性质的应用，考查了计算能力和数形结合思想，考查了空间想象能力和推理论证能力，属于中档题．