
分析 (1)求出函数的导数,求出f(0),f′(1)的值,从而求出函数的解析式即可;
(2)问题化为m=ex-x,x∈[-1,2],令h(x)=ex-x,x∈[-1,2],求出函数的导数,解关于导函数的不等式,求出h(x)的最小值,从而求出m的范围即可.
解答 解:(1)∵$f(x)=\frac{f'(1)}{e}{e^x}-f(0)x+\frac{1}{2}{x^2}$,
∴$f'(x)=\frac{f'(1)}{e}{e^x}-f(0)+x$,…(2分)
∴f'(1)=f'(1)-f(0)+1,
∴f(0)=1,…(3分)
∴$f(x)=\frac{f'(1)}{e}{e^x}-x+\frac{1}{2}{x^2}$,
∴$f(0)=\frac{f'(1)}{e}-0+0$,
∴f'(1)=e.…(4分)
可得:$f(x)={e^x}-x+\frac{1}{2}{x^2}$.…(6分)
(2)由$f(x)-\frac{1}{2}{x^2}-m=0$,化为m=ex-x,x∈[-1,2].
令h(x)=ex-x,x∈[-1,2],
∴h'(x)=ex-1,…(7分)
令h'(x)>0,解得0<x≤2,此时函数h(x)单调递增;
令h'(x)<0,解得-1≤x<0,此时函数h(x)单调递减.…(8分)
∴当x=0时,函数h(x)取得最小值,h(0)=1.…(9分)
而$h(-1)=1+\frac{1}{e},\;\;h(2)={e^2}-2$.…(10分)∵$1+\frac{1}{e}<{e^2}-2$.
又∵方程$f(x)-\frac{1}{2}{x^2}-m=0$在区间[-1,2]上恰有两个不同的实根,
∴$1<m≤1+\frac{1}{e}$,
∴实数m的取值范围是$({1,\;\;1+\frac{1}{e}}]$.…(12分)
点评 本题考查了求函数的解析式问题,考查函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>c>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
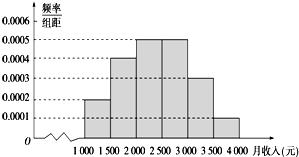 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com