
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率等于
,且离心率等于![]() .
.
(1)求椭圆的方程;
(2)若直线![]() 与椭圆交于
与椭圆交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点.若
两点.若![]() ,试求
,试求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意得关于a,b,c方程组,解方程组可得椭圆的方程;(2)根据垂径定理可求直线被圆解得弦长CD,根据韦达定理以及弦长公式可求AB,即得![]() 关于m的函数关系式,结合直线与圆相交条件得m取值范围,根据m范围求
关于m的函数关系式,结合直线与圆相交条件得m取值范围,根据m范围求![]() 的取值范围.
的取值范围.
试题解析:(1)由题意可得e=![]() =
=![]() ,
,
a2﹣b2=c2,
将M的坐标代入椭圆方程,可得
![]() +
+![]() =1,
=1,
解得a=2![]() ,b=c=2,
,b=c=2,
即有椭圆的方程为![]() +
+![]() =1;
=1;
(2)①O到直线y=x+m的距离为d=![]() ,
,
由弦长公式可得2=2![]() ,
,
解得m=±![]() ,
,
可得直线的方程为y=x±![]() ;
;
②由y=x+m代入椭圆方程x2+2y2=8,
可得3x2+4mx+2m2﹣8=0,
由判别式为△=16m2﹣12(2m2﹣8)>0,
化简可得m2<12,
由直线和圆相交的条件可得d<r,
即有![]() <
<![]() ,即为m2<4,
,即为m2<4,
综上可得m的范围是(﹣2,2).
设A(x1,y1),B(x2,y2),
可得x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,
,
即有弦长|AB|=![]()
![]()
=![]()
![]() =
=![]()
![]() ,
,
|CD|=2![]() =
=![]() ,
,
即有λ=![]() =
=![]()
![]() =
=![]()
![]() ,
,
由0<4﹣m2≤4,可得![]() ≥2,
≥2,
即有λ≥![]() .
.
则λ的取值范围是[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】已知f(x)=logmx(m为常数,m>0且m≠1),设f(a1),f(a2),…,f(an)(n∈N+)是首项为4,公差为2的等差数列.
(Ⅰ)求证:数列logman=2n+2,{an}是等比数列;
(Ⅱ)若bn=anf(an),记数列{bn}的前n项和为Sn , 当m= ![]() 时,求Sn .
时,求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB= ![]() ,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不交于同一点的三条直线l1:4x+y﹣4=0,l2:mx+y=0,l3:x﹣my﹣4=0
(1)当这三条直线不能围成三角形时,求实数m的值.
(2)当l3与l1 , l2都垂直时,求两垂足间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的焦点在x轴上,离心率等于 ![]() ,且过点(1,
,且过点(1, ![]() ). (Ⅰ)求椭圆C的标准方程;
). (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于M点,若 ![]() =λ1
=λ1 ![]() ,
, ![]() =λ2
=λ2 ![]() ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[﹣2,2]上的图象如图所示.给出下列四个命题: 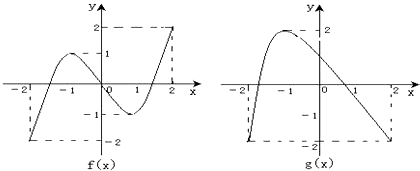
①方程f[g(x)]=0有且仅有6个根;
②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有5个根;
④方程g[g(x)]=0有且仅有4个根.
其中正确的命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点. 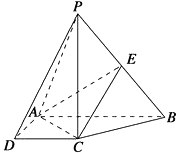
(1)求证:CE∥平面PAD;
(2)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com