Question

已知点G是△ABC的重心，A（0，-1），B（0，1）.在x轴上有一点M，满足||=||，=λ(λ∈R)（若△ABC的顶点坐标为?A(x₁,y₁),B(x₂,y₂),C(x₃,y₃)，则该三角形的重心坐标为G(,)).

（1）求点C的轨迹E的方程；

（2）设（1）中曲线E的左、右焦点分别为F₁、F₂，过点F₂的直线l交曲线E于P、Q两点，求△F₁PQ面积的最大值，并求出取最大值时直线l的方程.

Answer 1

解:（1）设C（x，y），则G(,).

∵=λ(λ∈R),∴GM∥AB.又M是x轴上一点，则M(,0),

又∵||=||,∴(=.整理得+y²=1(x≠0).

（2）由（1），知F₁(-,0),F₂(,0).

设直线l的方程为x=ty+,由（1），知x≠0,∴l不过点(0,±1).∴t≠±.

设P(x₁,y₁）,Q(x₂,y₂),将x=ty+代入x²+3y²=3,(t²+3)y²+2ty-1=0.∴Δ=8t²+4(t²+3)=12(t²+1)＞0恒成立.∴y₁+y₂=,y₁·y₂=.

∴|y₁-y₂|===.

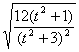∴=|F₁F₂|·|y₁-y₂|=|y₁-y₂|=2(t≠±).

∴=≤=.

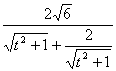当且仅当t₂+1=2，即t=±1时取“=”.

∴△F₁PQ的最大值为3,此时直线l的方程为x±y-2=0.