
【题目】已知数列{an}的前n项和为Sn , 满足a1= ![]() +3.
+3.
(1)证明:{an+1}是等比数列;
(2)求数列{an}的前n项和为Sn .
【答案】
(1)证明:∵Sn+1=Sn+4an+3,∴an+1=4an+3,变形为:an+1+1=4(an+1),
∴{an+1}是等比数列,首项为 ![]() ,公比为4;
,公比为4;
(2)解:由(1)可得:an+1= ![]() ×4n﹣1,∴an=
×4n﹣1,∴an= ![]() ﹣1.
﹣1.
∴数列{an}的前n项和为Sn= ![]() ﹣n=
﹣n= ![]() ﹣n.
﹣n.
【解析】(1)Sn+1=Sn+4an+3,可得an+1=4an+3,变形为:an+1+1=4(an+1),利用等比数列的定义即可证明.(2)由(1)可得:an+1= ![]() ×4n﹣1 , 即an=
×4n﹣1 , 即an= ![]() ﹣1.再利用等比数列的前n项和公式即可得出.
﹣1.再利用等比数列的前n项和公式即可得出.
【考点精析】认真审题,首先需要了解等比数列的通项公式(及其变式)(通项公式:![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,侧面
,侧面![]() 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面![]() 是
是![]() 的菱形,
的菱形,![]() 为
为![]() 的中点.
的中点.

(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 四点共面?若存在,指出点
四点共面?若存在,指出点![]() 的位置并说明;若不存在,请说明理由;
的位置并说明;若不存在,请说明理由;
(2)求点![]() 平面
平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-1:几何证明选讲]
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, ![]() OA为半径作圆.
OA为半径作圆.
(1)证明:直线A与⊙O相切;
(2)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,过棱AB的上一点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H

(1)求证:截面EFGH为平行四边形
(2)若P、Q在线段BD、AC上,![]() ,且P、F不重合,证明:PQ∥截面EFGH
,且P、F不重合,证明:PQ∥截面EFGH
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
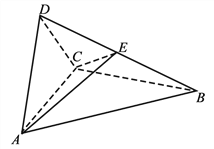
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
,![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以5为上界的有界函数,求实数
上是以5为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com