
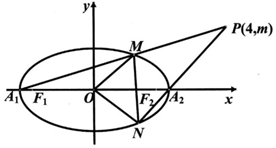
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.分析 (Ⅰ)由离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,列式计算a,b,即可得椭圆C的方程的方程
(Ⅱ)直线PA1,PA1的方程分别为:y=$\frac{m}{6}(x+2)$,y=$\frac{m}{2}(x-2)$,由$\left\{\begin{array}{l}{y=\frac{m}{6}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(9+m2)x2+4m2x+4m2-36=0,可得${x}_{M}=\frac{18-2{m}^{2}}{9+{m}^{2}}$,${y}_{M}=\frac{m}{6}({x}_{M}+2)$=$\frac{6m}{9+{m}^{2}}$,同理可得xN=$\frac{2{m}^{2}-2}{1+{m}^{2}}$,${y}_{N}=\frac{m}{2}({x}_{N}-2)$=$\frac{-2m}{1+{m}^{2}}$,直线MN的方程为:$y-\frac{-2m}{1+{m}^{2}}=\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})$,y=$\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})-\frac{2m}{1+{m}^{2}}$=$\frac{2m}{3-{m}^{2}}$$(x-\frac{2{m}^{2}-2}{1+{m}^{2}}-\frac{3-{m}^{2}}{1+{m}^{2}})$=$\frac{2m}{3-{m}^{2}}(x-1)$,可得直线MN过定点(1,0),故设MN的方程为:x=ty+1,
由$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(t2+4)y2+2ty-3=0,|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{t}^{2}+3}}{{t}^{2}+4}$,即△OMN的面积S=$\frac{1}{2}×1×$(y1-y2)=2$\frac{\sqrt{{t}^{2}+3}}{{t}^{2}+4}$利用函数单调性即可求出面积最大值.
解答 解:(Ⅰ)∵离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2c=2\sqrt{3}}\end{array}\right.$,∴a=2,c=$\sqrt{3}$,则b=1
∴椭圆C的方程的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)由(Ⅰ)得A1(-2,0),A2(2,0),
直线PA1,PA1的方程分别为:y=$\frac{m}{6}(x+2)$,y=$\frac{m}{2}(x-2)$
由$\left\{\begin{array}{l}{y=\frac{m}{6}(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(9+m2)x2+4m2x+4m2-36=0
∴-2+xM=$\frac{-4{m}^{2}}{9+{m}^{2}}$,可得.${x}_{M}=\frac{18-2{m}^{2}}{9+{m}^{2}}$,${y}_{M}=\frac{m}{6}({x}_{M}+2)$=$\frac{6m}{9+{m}^{2}}$
由$\left\{\begin{array}{l}{y=\frac{m}{2}(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得(1+m2)x2-4mx+4m2-4=0
∴2+xN=$\frac{4{m}^{2}}{1+{m}^{2}}$,可得xN=$\frac{2{m}^{2}-2}{1+{m}^{2}}$,${y}_{N}=\frac{m}{2}({x}_{N}-2)$=$\frac{-2m}{1+{m}^{2}}$
${k}_{MN}=\frac{{y}_{M}-{y}_{N}}{{x}_{M}-{x}_{N}}=\frac{2m}{3-{m}^{2}}$,
直线MN的方程为:$y-\frac{-2m}{1+{m}^{2}}=\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})$,
y=$\frac{2m}{3-{m}^{2}}(x-\frac{2{m}^{2}-2}{1+{m}^{2}})-\frac{2m}{1+{m}^{2}}$=$\frac{2m}{3-{m}^{2}}$$(x-\frac{2{m}^{2}-2}{1+{m}^{2}}-\frac{3-{m}^{2}}{1+{m}^{2}})$=$\frac{2m}{3-{m}^{2}}(x-1)$
可得直线MN过定点(1,0),故设MN的方程为:x=ty+1
由$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得(t2+4)y2+2ty-3=0
设M(x1,y1),N(x2,y2),则${y}_{1}+{y}_{2}=\frac{-2t}{{t}^{2}+4}$,${y}_{1}{y}_{2}=\frac{-3}{{t}^{2}+4}$
|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{{t}^{2}+3}}{{t}^{2}+4}$
∴△OMN的面积S=$\frac{1}{2}×1×$(y1-y2)=2$\frac{\sqrt{{t}^{2}+3}}{{t}^{2}+4}$
令$\sqrt{{t}^{2}+3}=d,(d≥\sqrt{3})$,则s=$\frac{2d}{{d}^{2}+1}=\frac{2}{d+\frac{1}{d}}$
∵$d≥\sqrt{3}$,且函数f(d)=d+$\frac{1}{d}$在[$\sqrt{3}$,+∞)递增,
∴当d=$\sqrt{3}$,s取得最小值$\frac{\sqrt{3}}{2}$
点评 本题考查了椭圆的方程,直线与椭圆的位置关系,方程思想,转化思想,考查了运算能力,属于难题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | -2017 | C. | -2015 | D. | -2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com