
分析 构造函数f(m),转化为一元一次函数恒成立问题,进行求解即可.
解答 解:不等式x2-(2+m)x+m-1>0等价为(x+1)m+x2-2x-1>0对任意的m∈[-1,1]恒成立,
设f(m)=(x+1)m+x2-2x-1,
则等价为$\left\{\begin{array}{l}{f(1)>0}\\{f(-1)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}-3x>0}\\{{x}^{2}-x-2>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>3或x<0}\\{x>2或x<-1}\end{array}\right.$,即x>3或x<-1,
故答案为:(-∞,-1)∪(3,+∞)
点评 本题主要考查不等式恒成立问题,利用参数转化法,转化为以m为变量的不等式是解决本题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
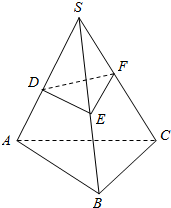 如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.
如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y=0 | B. | $x-2y-\frac{5}{2}=0$ | C. | 2x-y-2=0 | D. | $x-4y-\frac{9}{2}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com