
| A. | ①② | B. | ③④ | C. | ②④ | D. | ②③ |
分析 由条件利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性以及它们的图象的对称性,得出结论.
解答 解:对于函数f(x)=$2cos(2x+\frac{π}{6})$,它的最小正周期为$\frac{2π}{2}$=π,故①不正确.
当x=$\frac{π}{6}$时,函数f(x)=2cos$\frac{π}{2}$=0,故函数f(x)的图象关于点$(\frac{π}{6},0)$对称,故②正确.
y=2cos2x的图象向左平移$\frac{π}{6}$个单位得到函数y=2cos2(x+$\frac{π}{6}$)=2cos(2x+$\frac{π}{3}$),故③不正确.
函数$f(x+\frac{π}{6})$=2cos[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=2cos(2x+$\frac{π}{2}$)=-sin2x,是奇函数,故④正确.
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性以及它们的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
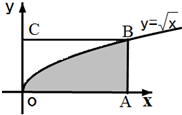 如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 | 频率 | “光盘族”占本组比例 |
| 第1组 | [25,30) | 50 | 0.05 | 30% |
| 第2组 | [30,35) | 100 | 0.10 | 30% |
| 第3组 | [35,40) | 150 | 0.15 | 40% |
| 第4组 | [40,45) | 200 | 0.20 | 50% |
| 第5组 | [45,50) | a | b | 65% |
| 第6组 | [50,55) | 200 | 0.20 | 60% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与g(x)=x-1 | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=$\sqrt{-2{x}^{3}}$与g(x)=x$\sqrt{-2x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com