
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与g(x)=x-1 | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=$\sqrt{-2{x}^{3}}$与g(x)=x$\sqrt{-2x}$ |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:A.f(x)的定义域为{x|x≠1},所以两个函数的定义域不同,所以两个函数不是同一个函数.
B.f(x)=$\sqrt{{x}^{2}}$-1=|x|-1,函数f(x)与g(x)的对应法则不相同.所以两个函数的不能表示同一个函数.
C.因为函数f(x)的定义域为{x|x≠-3},G(x)的定义域为{x|x≠-3},两个函数的定义域相同,对应法则相同,所以两个函数的能表示同一个函数.
D.函数f(x)的定义域为{x|x≤0},f(x)=-xx$\sqrt{-2x}$,g(x)的定义域为{x|x≤0},所以两个函数的定义域相同,f(x)与g(x)的对应法则不相同,所以两个函数不是同一个函数.
故选:C.
点评 本题主要考查两个函数是否为同一函数,利用函数的定义域和对应法则是否相同是解决本题的关键,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是正方体的平面展开图,在这个正方体中:
如图是正方体的平面展开图,在这个正方体中:| A. | ①②③ | B. | ②④ | C. | ②③④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2或a>2 | B. | a≤-2或a≥2 | C. | -2<a<2 | D. | -2≤a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
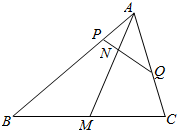 如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com