
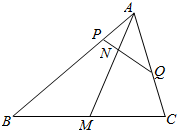
 如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.分析 (1)分别过点B,C做PQ的平行线,交AM的延长线于D,E,则△BDM≌△CEM,利用PQ∥BD得比例,即可证明结论;
(2)利用(1)的结论,即可求$\frac{MN}{NA}$的值.
解答  (1)证明:分别过点B,C做PQ的平行线,交AM的延长线于D,E,则△BDM≌△CEM,
(1)证明:分别过点B,C做PQ的平行线,交AM的延长线于D,E,则△BDM≌△CEM,
∴DM=EM,
∵PQ∥BD,
∴$\frac{PB}{PA}=\frac{ND}{AN}$①
同理$\frac{QC}{QA}$=$\frac{NE}{AN}$②
①+②得$\frac{PB}{PA}$+$\frac{QC}{QA}$=$\frac{2MN}{NA}$,
(2)解:∵$\frac{AP}{PB}$=m,$\frac{AQ}{QC}$=n,
∴$\frac{1}{m}$+$\frac{1}{n}$=$\frac{2MN}{NA}$,
∴$\frac{MN}{NA}$=$\frac{m+n}{2mn}$.
点评 本题考查比例线段,考查学生分析解决问题的能力,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与g(x)=x-1 | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=$\sqrt{-2{x}^{3}}$与g(x)=x$\sqrt{-2x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
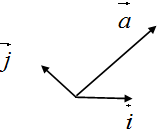 如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$
如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x≤5} | B. | {x|1≤x≤6} | C. | {x|1≤x≤3} | D. | {x|3≤x≤6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com