
分析 证明$\frac{1}{\sqrt{{k}^{3}}}$=$\frac{1}{\sqrt{{k}^{2}•k}}$<$\frac{1}{\sqrt{({k}^{2}-\frac{1}{4})•k}}$=$\frac{\sqrt{2k-1}+\sqrt{2k+1}}{\sqrt{k}}$•($\frac{1}{\sqrt{2k-1}}$-$\frac{1}{\sqrt{2k+1}}$)<2$\sqrt{2}$•($\frac{1}{\sqrt{2k-1}}$-$\frac{1}{\sqrt{2k+1}}$),再叠加,即可证明结论.
解答 证明:∵$(\sqrt{2k-1}+\sqrt{2k+1})^{2}$=4k+2$\sqrt{4{k}^{2}-1}$<4k+4k=8k.
∴$\frac{\sqrt{2k-1}+\sqrt{2k+1}}{\sqrt{k}}$<2$\sqrt{2}$,
∴$\frac{1}{\sqrt{{k}^{3}}}$=$\frac{1}{\sqrt{{k}^{2}•k}}$<$\frac{1}{\sqrt{({k}^{2}-\frac{1}{4})•k}}$=$\frac{\sqrt{2k-1}+\sqrt{2k+1}}{\sqrt{k}}$•($\frac{1}{\sqrt{2k-1}}$-$\frac{1}{\sqrt{2k+1}}$)<2$\sqrt{2}$•($\frac{1}{\sqrt{2k-1}}$-$\frac{1}{\sqrt{2k+1}}$).
∴1+$\frac{1}{2\sqrt{2}}$+$\frac{1}{3\sqrt{3}}$+…+$\frac{1}{n\sqrt{n}}$<2$\sqrt{2}$•[(1-$\frac{1}{\sqrt{3}}$)+…+($\frac{1}{\sqrt{2n-1}}$-$\frac{1}{\sqrt{2n+1}}$)]=2$\sqrt{2}$•(1-$\frac{1}{\sqrt{2n+1}}$)$<2\sqrt{2}$<3,
∴1+$\frac{1}{2\sqrt{2}}$+$\frac{1}{3\sqrt{3}}$+…+$\frac{1}{n\sqrt{n}}$<3(n∈N*)
点评 本题考查不等式的证明,考查放缩法的运用,正确放缩是关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | a<-2或a>2 | B. | a≤-2或a≥2 | C. | -2<a<2 | D. | -2≤a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
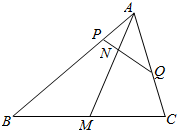 如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图.已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空集 | B. | {1} | C. | {0,1,2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)是函数的最小值 | B. | f(8)是函数的最小值 | ||
| C. | f(6)是函数的最大值 | D. | 以上结论都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com