
(1)若a=-2时,函数h(x)=f(x)-g(x)在其定义域内是增函数,求b的取值范围;
(2)在(1)的结论下,设函数φ(x)=e2x+bex,x∈[0,ln2],求函数φ(x)的最小值;
(3)设函数f(x)的图象C1与函数g(x)的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
解:(1)依题意:h(x)=lnx+x2-bx.∵h(x)在(0,+∞)上是增函数,
∴h(x)=![]() +2x-b≥0对x∈(0,+∞)恒成立.
+2x-b≥0对x∈(0,+∞)恒成立.
∴b≤![]() +2x.∵x>0,则
+2x.∵x>0,则![]() +2x≥2
+2x≥2![]() .∴b的取值范围为(-∞,2
.∴b的取值范围为(-∞,2![]() ].
].
(2)设t=ex,则函数化为y=t2+bt,t∈[1,2].∵y=(t+![]() )2
)2![]() ,
,
∴当![]() ≤1,即-2≤b≤2
≤1,即-2≤b≤2![]() 时,函数y在[1,2]上为增函数.
时,函数y在[1,2]上为增函数.
当t=1时,ymin=b+1.
当1<![]() <2,即-4<b<-2时,当t=
<2,即-4<b<-2时,当t=![]() 时,ymin=
时,ymin=![]() ;
;
当![]() ≥2,即b≤-4时,函数y在[1,2]上为减函数,
≥2,即b≤-4时,函数y在[1,2]上为减函数,
当t=2时,ymin=4+2b.
综上所述,当-2≤b≤2![]() 时,φ(x)的最小值为b+1.
时,φ(x)的最小值为b+1.
当-4<b<-2时,φ(x)的最小值为![]() .当b≤-4时,φ(x)的最小值为4+2b.
.当b≤-4时,φ(x)的最小值为4+2b.
(3)设点P、Q的坐标是(x1,y1),(x2,y2),且0<x1<x2.
则点M、N的横坐标为x=![]() .C1在点M处的切线斜率为k1=
.C1在点M处的切线斜率为k1=![]() .
.
C2在点N处的切线斜率为k2=![]() +b.
+b.
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2,
即![]() =+b.则
=+b.则![]() =
=![]() +b(x2-x1)
+b(x2-x1)
=(![]() x22+bx2)-(
x22+bx2)-(![]() x12+bx1)=y2-y1=lnx2-lnx1=ln
x12+bx1)=y2-y1=lnx2-lnx1=ln![]() .∴ln
.∴ln![]() =
=![]() =
=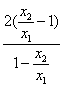 .
.
设u=![]() >1,则lnu=
>1,则lnu=![]() ,u>1.①
,u>1.①
令r(u)=lnu![]() ,u>1.则r′(u)=
,u>1.则r′(u)=![]() .∵u>1,∴r′(u)>0.
.∵u>1,∴r′(u)>0.
∴r(u)在[1,+∞)上单调递增,故r(u)>r(1)=0.
则lnu>![]() .这与①矛盾,假设不成立.
.这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 3 |
| 2 |
| f′(x) |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com