
已知函数 ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且 .
.
⑴指出函数 的单调区间;
的单调区间;
⑵若函数 的图象在点
的图象在点 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值;
⑶若函数 的图象在点
的图象在点 处的切线重合,求
处的切线重合,求 的取值范围.
的取值范围.
(1)单调减区间为 ,单调增区间为
,单调增区间为 ;(2)1;(3)
;(2)1;(3) .
.
解析试题分析:(1)根据基本初等函数的性质知,分段函数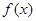 在
在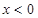 时是二次函数的一部分,有两个单调区间:增区间
时是二次函数的一部分,有两个单调区间:增区间 ,减区间
,减区间 ,
, 时是对数函数,只有一个单调增区间
时是对数函数,只有一个单调增区间 ;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有
;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有 ,由于
,由于 ,
, 两点在
两点在 轴的左边,
轴的左边, ,因此有
,因此有 ,显然有
,显然有 ,
, 可以表示为关于
可以表示为关于 的函数,从而求出最小值(
的函数,从而求出最小值( ,
,
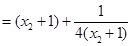 应用基本不等式即可得解)也可以直接凑配出基本不等式的形式,
应用基本不等式即可得解)也可以直接凑配出基本不等式的形式, =
= 利用基本不等式);(3)这里我们首先分析
利用基本不等式);(3)这里我们首先分析 所处范围,结合图象易知
所处范围,结合图象易知 不可能在同一单调区间,只能是
不可能在同一单调区间,只能是 ,那么我们可得出
,那么我们可得出 两点处的切线方程分别为
两点处的切线方程分别为 ,
, ,两条切线相同,则有
,两条切线相同,则有 ,于是可把
,于是可把 表示为
表示为 (或者
(或者 )的函数,把求
)的函数,把求 匠范围转化为求函数的值域.
匠范围转化为求函数的值域.
试题解析:(1)单调减区间为 ,单调增区间为
,单调增区间为 4分
4分
(2) ,
,
当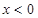 时,因为
时,因为 ,所以
,所以 .8分
.8分
∴
当且仅当 时等号成立,
时等号成立,
∴ 的最小值为1.10分
的最小值为1.10分
(3)当 或
或 时,
时, ,故
,故
当 时,函数
时,函数 的图象在点
的图象在点 的切线方程为
的切线方程为
即
当 时,函数
时,函数 在
在 切线方程为
切线方程为
两切线重合的充要条件是 13分
13分
由①及 知
知
由①②得
又 ,与
,与 在
在 都为减函数.
都为减函数.
∴ 16分
16分
考点:(1)单调区间;(2)函数图象的切线及基本不等式;(3)切线与函数的值域.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=x3+ax-2,(a R).
R).
(l)若f(x)在区间(1,+ )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;
(2)若 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;
(3)若 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻x的关系为
与时刻x的关系为 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且 ,若用每天
,若用每天 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作 .
.
(Ⅰ)令 ,求t的取值范围;
,求t的取值范围;
(Ⅱ)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点 ,交曲线于点
,交曲线于点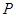 ,设
,设 .
.
(1)将△ (
( 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数 ;
;
(2)若在 处,
处, 取得最小值,求此时
取得最小值,求此时 的值及
的值及 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com