
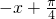 )=f(
)=f(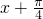 ),则下列函数中,符合上述条件的有 ________.(填序号)
),则下列函数中,符合上述条件的有 ________.(填序号) );
); );④f(x)=cos(
);④f(x)=cos(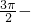 4x).
4x). ,再利用诱导公式对选项中解析式进行化简,根据正弦(余弦)函数的奇偶性和对称轴方程进行逐一判断.
,再利用诱导公式对选项中解析式进行化简,根据正弦(余弦)函数的奇偶性和对称轴方程进行逐一判断. ,
, 代入得,4x=π,则
代入得,4x=π,则 是函数的对称轴,故①符合条件;
是函数的对称轴,故①符合条件; )=cos2x是偶函数,把
)=cos2x是偶函数,把 代入得,2x=
代入得,2x= ,则
,则 不是函数的对称轴,故②不符合题意;
不是函数的对称轴,故②不符合题意; )=cos4x,同①分析,故③符合题意;
)=cos4x,同①分析,故③符合题意;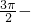 4x)=-sin4x是奇函数,故④不符合题意.
4x)=-sin4x是奇函数,故④不符合题意.

科目:高中数学 来源: 题型:解答题
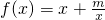 ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).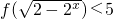 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
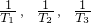 ,并证明
,并证明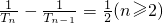 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 件货储存在仓库里,库存费以每件20元计算,要使一年的运费和库存费最省,每次进货量x应是多少?
件货储存在仓库里,库存费以每件20元计算,要使一年的运费和库存费最省,每次进货量x应是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com